4x-2-y-y-0-x-gt-0-

Question Number 103037 by bramlex last updated on 12/Jul/20

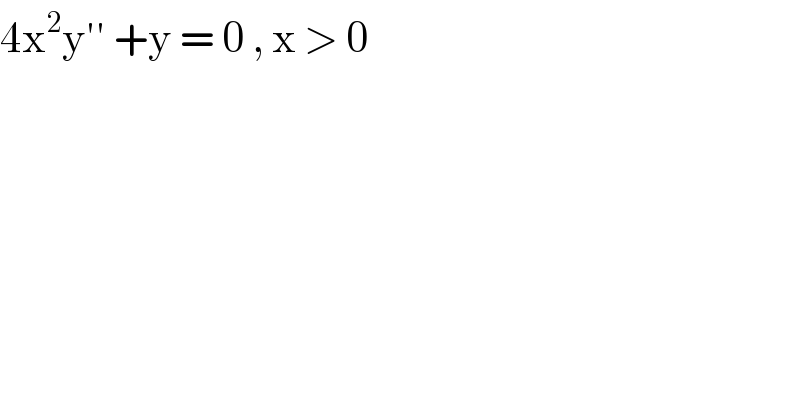
{4 x}^{2} y^{″} + y = 0, x > 0

Answered by maths mind last updated on 12/Jul/20

l e t y = x^{t}

\Rightarrow 4 x^{2} (t (t - 1)) x^{t - 2} + x^{t} = 0

\Leftrightarrow (4 t^{2} - 4 t + 1) x^{t} = 0

\Leftrightarrow {(2 t - 1)}^{2} x^{t} = 0 \Rightarrow t = \frac{1}{2}

l e t y = \sqrt{x} z

\Rightarrow y^{'} = z^{'} \sqrt{x} + \frac{z}{2 \sqrt{x}}, y^{″} = \frac{z^{'}}{\sqrt{x}} + z^{″} \sqrt{x} - \frac{z}{4 x \sqrt{x}}

\Leftrightarrow 4 x \sqrt{x} z^{'} + 4 x^{2} \sqrt{x} z^{″} - z \sqrt{x} + z \sqrt{x} = 0

\Rightarrow z^{'} + {x z}^{″} = 0

\Rightarrow \frac{z^{″}}{z^{'}} = - \frac{1}{x} \Rightarrow l n (z^{'}) = - l n (x) + c

\Rightarrow z^{'} = \frac{k}{x} \Rightarrow z = k l n (x) + c

\Rightarrow y = (k l n (x) + c) \sqrt{x}