Question Number 65307 by divyajyoti last updated on 28/Jul/19
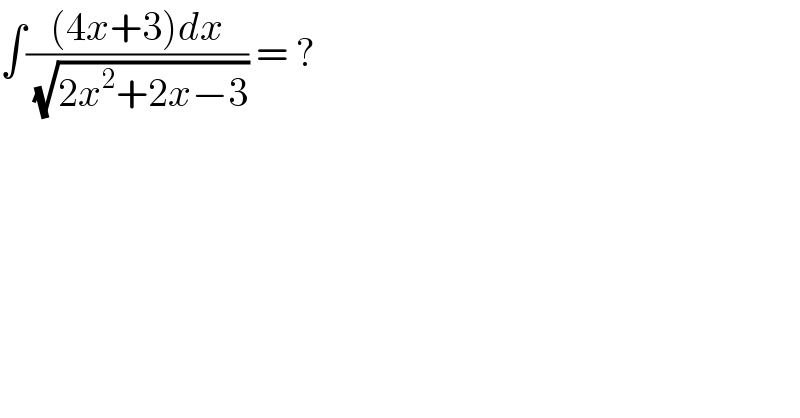
$$\int\frac{\left(\mathrm{4}{x}+\mathrm{3}\right){dx}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}}\:=\:?\: \\ $$
Answered by divyajyoti last updated on 28/Jul/19
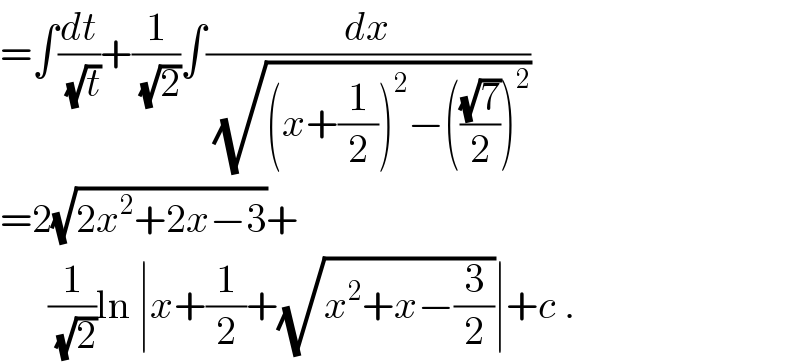
$$=\int\frac{{dt}}{\:\sqrt{{t}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dx}}{\:\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)^{\mathrm{2}} }} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}+ \\ $$$$\:\:\:\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} +{x}−\frac{\mathrm{3}}{\mathrm{2}}}\mid+{c}\:. \\ $$
Commented by divyajyoti last updated on 28/Jul/19

$$\left({new}\:{user}\right){I}\:{solved}\:{it}\:{myself},\:{hahaha}! \\ $$$${just}\:{learning}\:{how}\:{to}\:{use}\:{the}\:{app}. \\ $$
