Question Number 124540 by micelle last updated on 04/Dec/20
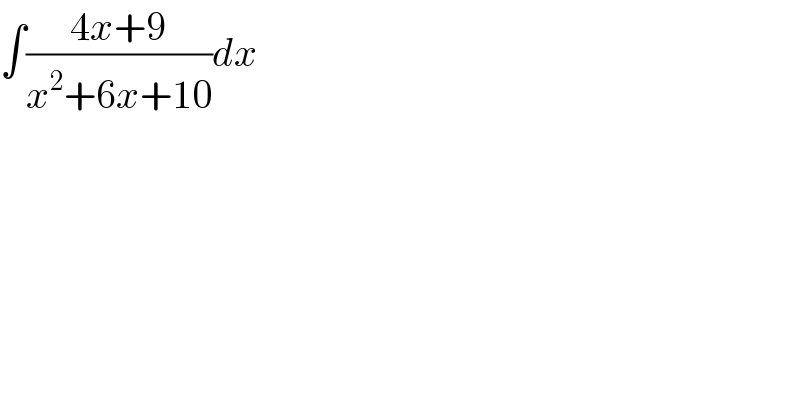
$$\int\frac{\mathrm{4}{x}+\mathrm{9}}{{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{10}}{dx} \\ $$
Answered by Ar Brandon last updated on 04/Dec/20
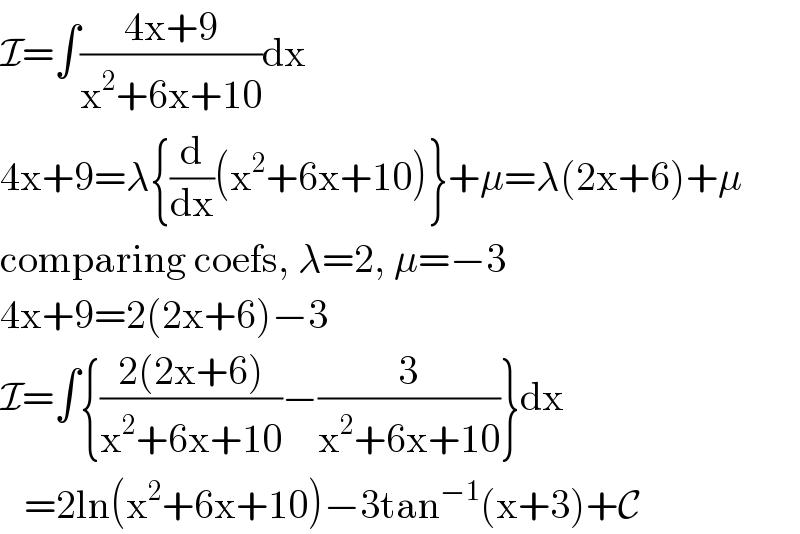
$$\mathcal{I}=\int\frac{\mathrm{4x}+\mathrm{9}}{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{10}}\mathrm{dx} \\ $$$$\mathrm{4x}+\mathrm{9}=\lambda\left\{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{10}\right)\right\}+\mu=\lambda\left(\mathrm{2x}+\mathrm{6}\right)+\mu \\ $$$$\mathrm{comparing}\:\mathrm{coefs},\:\lambda=\mathrm{2},\:\mu=−\mathrm{3} \\ $$$$\mathrm{4x}+\mathrm{9}=\mathrm{2}\left(\mathrm{2x}+\mathrm{6}\right)−\mathrm{3} \\ $$$$\mathcal{I}=\int\left\{\frac{\mathrm{2}\left(\mathrm{2x}+\mathrm{6}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{10}}−\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{10}}\right\}\mathrm{dx} \\ $$$$\:\:\:=\mathrm{2ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{10}\right)−\mathrm{3tan}^{−\mathrm{1}} \left(\mathrm{x}+\mathrm{3}\right)+\mathcal{C} \\ $$
Answered by mathmax by abdo last updated on 04/Dec/20
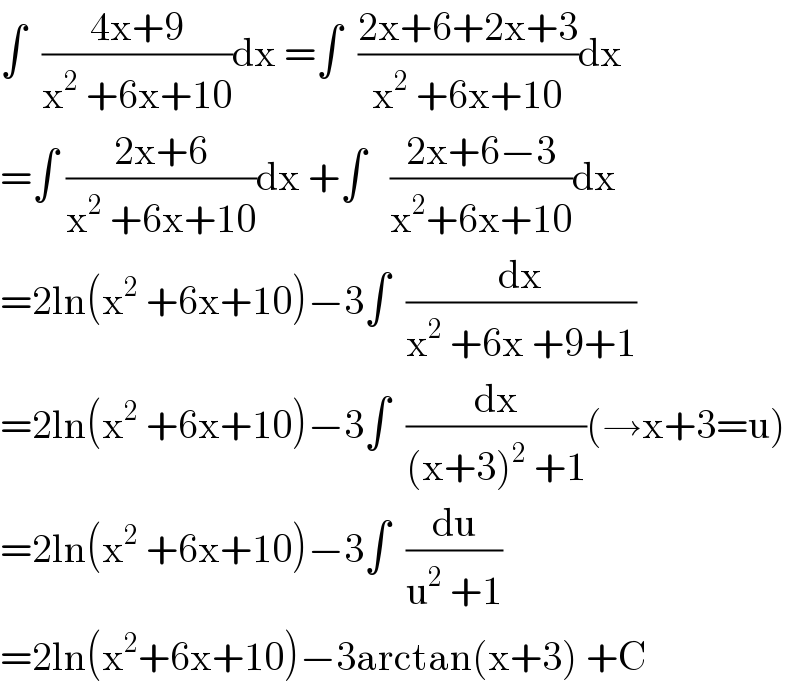
$$\int\:\:\frac{\mathrm{4x}+\mathrm{9}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{6x}+\mathrm{10}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{2x}+\mathrm{6}+\mathrm{2x}+\mathrm{3}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{6x}+\mathrm{10}}\mathrm{dx} \\ $$$$=\int\:\frac{\mathrm{2x}+\mathrm{6}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{6x}+\mathrm{10}}\mathrm{dx}\:+\int\:\:\:\frac{\mathrm{2x}+\mathrm{6}−\mathrm{3}}{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{10}}\mathrm{dx} \\ $$$$=\mathrm{2ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{6x}+\mathrm{10}\right)−\mathrm{3}\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{6x}\:+\mathrm{9}+\mathrm{1}} \\ $$$$=\mathrm{2ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{6x}+\mathrm{10}\right)−\mathrm{3}\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} \:+\mathrm{1}}\left(\rightarrow\mathrm{x}+\mathrm{3}=\mathrm{u}\right) \\ $$$$=\mathrm{2ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{6x}+\mathrm{10}\right)−\mathrm{3}\int\:\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\: \\ $$$$=\mathrm{2ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{10}\right)−\mathrm{3arctan}\left(\mathrm{x}+\mathrm{3}\right)\:+\mathrm{C} \\ $$
