Question Number 60853 by Tony Lin last updated on 26/May/19

$$\sqrt{\mathrm{5}−\mathrm{12}{i}}+\sqrt{\mathrm{5}+\mathrm{12}{i}}=? \\ $$
Answered by tanmay last updated on 26/May/19
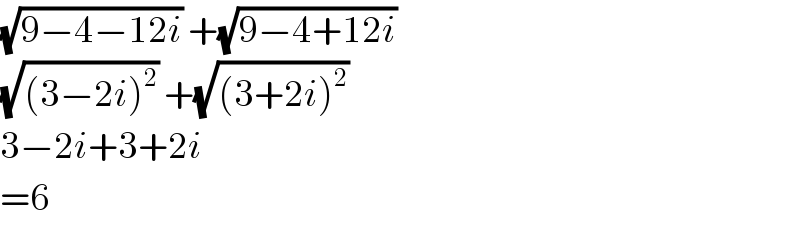
$$\sqrt{\mathrm{9}−\mathrm{4}−\mathrm{12}{i}}\:+\sqrt{\mathrm{9}−\mathrm{4}+\mathrm{12}{i}}\: \\ $$$$\sqrt{\left(\mathrm{3}−\mathrm{2}{i}\right)^{\mathrm{2}} }\:+\sqrt{\left(\mathrm{3}+\mathrm{2}{i}\right)^{\mathrm{2}} }\: \\ $$$$\mathrm{3}−\mathrm{2}{i}+\mathrm{3}+\mathrm{2}{i} \\ $$$$=\mathrm{6} \\ $$
Commented by Tony Lin last updated on 26/May/19
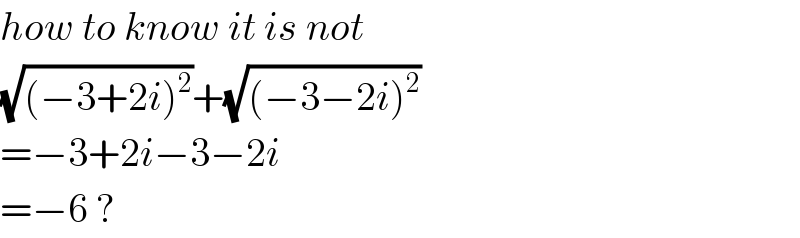
$${how}\:{to}\:{know}\:{it}\:{is}\:{not} \\ $$$$\sqrt{\left(−\mathrm{3}+\mathrm{2}{i}\right)^{\mathrm{2}} }+\sqrt{\left(−\mathrm{3}−\mathrm{2}{i}\right)^{\mathrm{2}} } \\ $$$$=−\mathrm{3}+\mathrm{2}{i}−\mathrm{3}−\mathrm{2}{i} \\ $$$$=−\mathrm{6}\:? \\ $$
Answered by MJS last updated on 26/May/19

$$\mathrm{5}−\mathrm{12i}=\mathrm{13e}^{\mathrm{i}\:\mathrm{arctan}\:−\frac{\mathrm{12}}{\mathrm{5}}} \\ $$$$\sqrt{\mathrm{5}−\mathrm{12i}}=\sqrt{\mathrm{13}}\mathrm{e}^{\mathrm{i}\:\frac{\mathrm{arctan}\:−\frac{\mathrm{12}}{\mathrm{5}}}{\mathrm{2}}} =\mathrm{3}−\mathrm{2i} \\ $$$$\mathrm{5}+\mathrm{12i}=\mathrm{13e}^{\mathrm{i}\:\mathrm{arctan}\:\frac{\mathrm{12}}{\mathrm{5}}} \\ $$$$\sqrt{\mathrm{5}+\mathrm{12i}}=\sqrt{\mathrm{13}}\mathrm{e}^{\mathrm{i}\frac{\mathrm{arctan}\:\frac{\mathrm{12}}{\mathrm{5}}}{\mathrm{2}}} =\mathrm{3}+\mathrm{2i} \\ $$$$\mathrm{the}\:\mathrm{root}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{as}\:\mathrm{the}\:\mathrm{principal}\:\mathrm{value} \\ $$$${r}\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{with}\:−\pi\leqslant\theta<\pi\:\mathrm{and}\:{r}\in\mathbb{R}^{+} \\ $$$$\Rightarrow\:\sqrt{{r}\mathrm{e}^{\mathrm{i}\theta} }=\sqrt{{r}}\mathrm{e}^{\mathrm{i}\frac{\theta}{\mathrm{2}}} \:\mathrm{with}\:−\frac{\pi}{\mathrm{2}}\leqslant\frac{\theta}{\mathrm{2}}<\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{unique} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{different}\:\mathrm{of}\:\mathrm{solving}\:\mathrm{an}\:\mathrm{equation}\:\mathrm{to}\:\mathrm{find} \\ $$$$\mathrm{all}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:\mathrm{an}\:\mathrm{unknown} \\ $$
Commented by Tony Lin last updated on 27/May/19
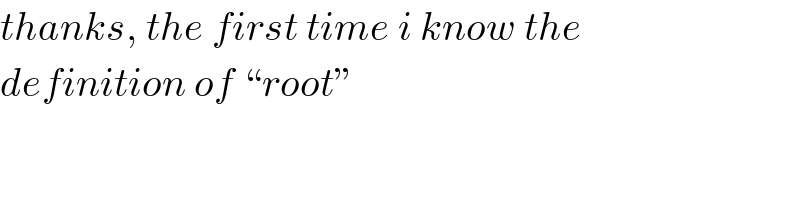
$${thanks},\:{the}\:{first}\:{time}\:{i}\:{know}\:{the}\: \\ $$$${definition}\:{of}\:“{root}'' \\ $$
