Question Number 146244 by mathdanisur last updated on 12/Jul/21
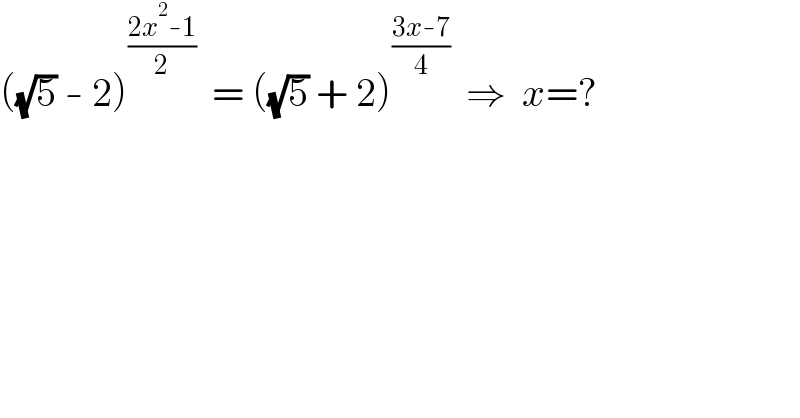
$$\left(\sqrt{\mathrm{5}}\:-\:\mathrm{2}\right)^{\frac{\mathrm{2}{x}^{\mathrm{2}} -\mathrm{1}}{\mathrm{2}}} \:\:=\:\left(\sqrt{\mathrm{5}}\:+\:\mathrm{2}\right)^{\frac{\mathrm{3}{x}-\mathrm{7}}{\mathrm{4}}} \:\:\Rightarrow\:\:{x}=? \\ $$
Answered by gsk2684 last updated on 12/Jul/21

$${use}\:\sqrt{\mathrm{5}}−\mathrm{2}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{2}} \\ $$$${compare}\:{exponents} \\ $$
Answered by Olaf_Thorendsen last updated on 12/Jul/21
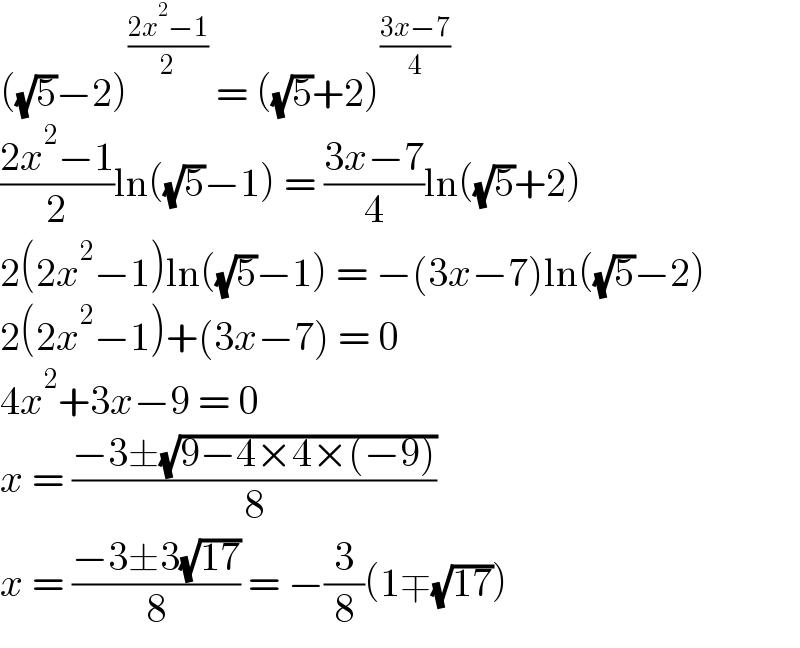
$$\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)^{\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}} \:=\:\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)^{\frac{\mathrm{3}{x}−\mathrm{7}}{\mathrm{4}}} \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\:=\:\frac{\mathrm{3}{x}−\mathrm{7}}{\mathrm{4}}\mathrm{ln}\left(\sqrt{\mathrm{5}}+\mathrm{2}\right) \\ $$$$\mathrm{2}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{ln}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\:=\:−\left(\mathrm{3}{x}−\mathrm{7}\right)\mathrm{ln}\left(\sqrt{\mathrm{5}}−\mathrm{2}\right) \\ $$$$\mathrm{2}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)+\left(\mathrm{3}{x}−\mathrm{7}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{9}\:=\:\mathrm{0} \\ $$$${x}\:=\:\frac{−\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{4}×\mathrm{4}×\left(−\mathrm{9}\right)}}{\mathrm{8}} \\ $$$${x}\:=\:\frac{−\mathrm{3}\pm\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{8}}\:=\:−\frac{\mathrm{3}}{\mathrm{8}}\left(\mathrm{1}\mp\sqrt{\mathrm{17}}\right) \\ $$
Commented by mathdanisur last updated on 12/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
