Question Number 113261 by Aina Samuel Temidayo last updated on 12/Sep/20
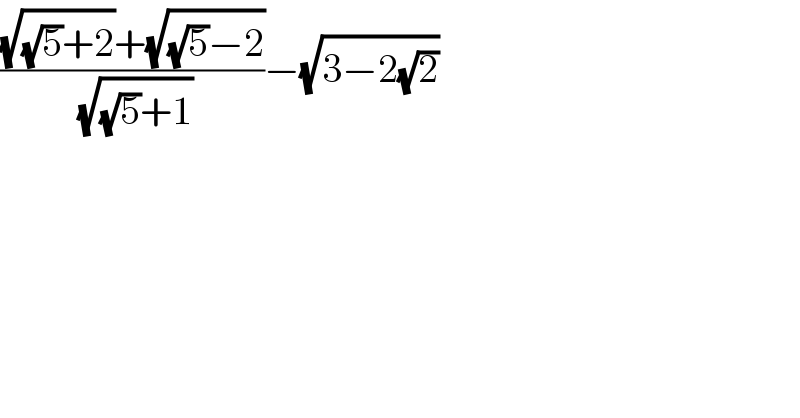
$$\frac{\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}}+\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}}{\:\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}−\sqrt{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Answered by som(math1967) last updated on 12/Sep/20
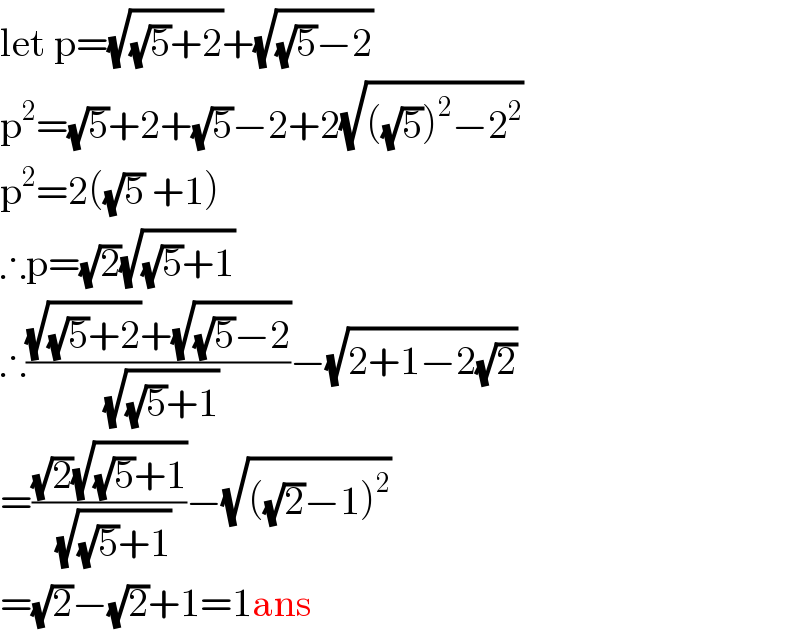
$$\mathrm{let}\:\mathrm{p}=\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}}+\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}} \\ $$$$\mathrm{p}^{\mathrm{2}} =\sqrt{\mathrm{5}}+\mathrm{2}+\sqrt{\mathrm{5}}−\mathrm{2}+\mathrm{2}\sqrt{\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} } \\ $$$$\mathrm{p}^{\mathrm{2}} =\mathrm{2}\left(\sqrt{\mathrm{5}}\:+\mathrm{1}\right) \\ $$$$\therefore\mathrm{p}=\sqrt{\mathrm{2}}\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}} \\ $$$$\therefore\frac{\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}}+\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}}{\:\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}−\sqrt{\mathrm{2}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$=\frac{\sqrt{\mathrm{2}}\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}{\:\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}−\sqrt{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}}+\mathrm{1}=\mathrm{1ans} \\ $$
Commented by Aina Samuel Temidayo last updated on 12/Sep/20

$$\mathrm{Thanks}. \\ $$
