Question Number 157913 by HongKing last updated on 29/Oct/21
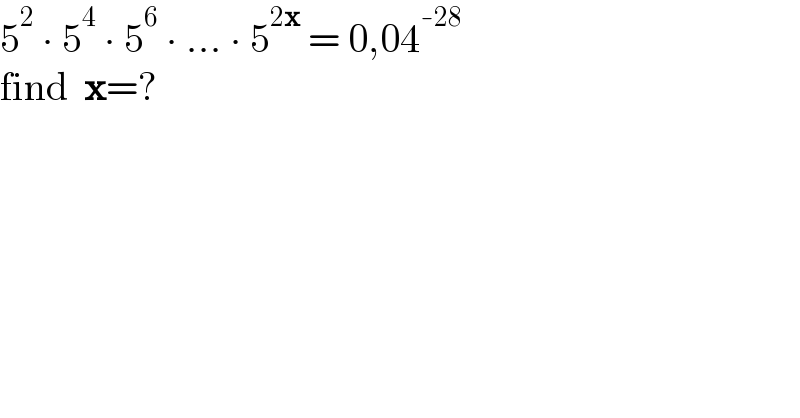
$$\mathrm{5}^{\mathrm{2}} \:\centerdot\:\mathrm{5}^{\mathrm{4}} \:\centerdot\:\mathrm{5}^{\mathrm{6}} \:\centerdot\:…\:\centerdot\:\mathrm{5}^{\mathrm{2}\boldsymbol{\mathrm{x}}} \:=\:\mathrm{0},\mathrm{04}^{-\mathrm{28}} \\ $$$$\mathrm{find}\:\:\boldsymbol{\mathrm{x}}=? \\ $$
Answered by Rasheed.Sindhi last updated on 29/Oct/21

$$\mathrm{5}^{\mathrm{2}} \:\centerdot\:\mathrm{5}^{\mathrm{4}} \:\centerdot\:\mathrm{5}^{\mathrm{6}} \:\centerdot\:…\:\centerdot\:\mathrm{5}^{\mathrm{2}\boldsymbol{\mathrm{x}}} \:=\:\mathrm{0},\mathrm{04}^{-\mathrm{28}} \\ $$$$\mathrm{5}^{\mathrm{2}+\mathrm{4}+\mathrm{6}+…+\mathrm{2}{x}} =\mathrm{0}.\mathrm{04}^{−\mathrm{28}} \\ $$$$\mathrm{5}^{\mathrm{2}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\mathrm{x}\right)} =\left(\frac{\mathrm{4}}{\mathrm{100}}\right)^{−\mathrm{28}} \\ $$$$\mathrm{5}^{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)} =\left(\mathrm{5}^{−\mathrm{2}} \right)^{−\mathrm{28}} =\mathrm{5}^{\mathrm{56}} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}=\mathrm{56} \\ $$$$\left(\mathrm{x}+\mathrm{8}\right)\left(\mathrm{x}−\mathrm{7}\right)=\mathrm{0} \\ $$$$\mathrm{x}=−\mathrm{8},\mathrm{7} \\ $$$$\mathrm{If}\:\mathrm{x}\:\mathrm{is}\:\mathrm{number}\:\mathrm{of}\:\mathrm{terms}\:\mathrm{then}\:−\mathrm{8}\:\mathrm{is} \\ $$$$\mathrm{rejectable}\:\mathrm{and}\:\mathrm{x}=\mathrm{7} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Nov/21

$${Please}\:{confirm}\:{the}\:{answer}. \\ $$
Commented by HongKing last updated on 04/Nov/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{perfect} \\ $$
