Question Number 144249 by mathdanisur last updated on 23/Jun/21
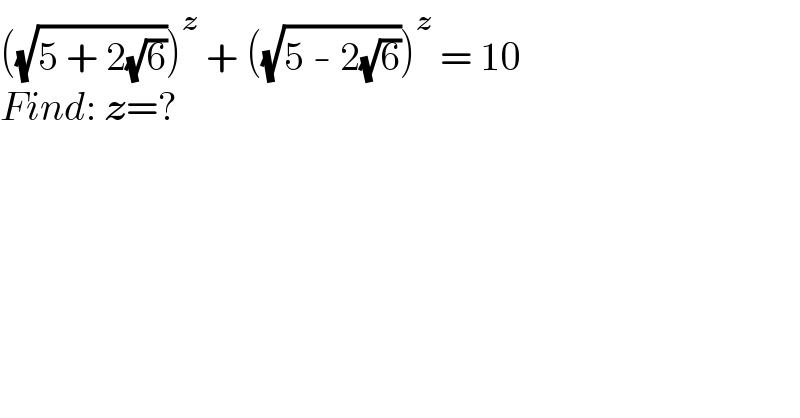
$$\left(\sqrt{\mathrm{5}\:+\:\mathrm{2}\sqrt{\mathrm{6}}}\right)^{\boldsymbol{{z}}} \:+\:\left(\sqrt{\mathrm{5}\:-\:\mathrm{2}\sqrt{\mathrm{6}}}\right)^{\boldsymbol{{z}}} \:=\:\mathrm{10} \\ $$$${Find}:\:\boldsymbol{{z}}=? \\ $$
Answered by Dwaipayan Shikari last updated on 23/Jun/21

$$\mathrm{2} \\ $$
Commented by mathdanisur last updated on 23/Jun/21
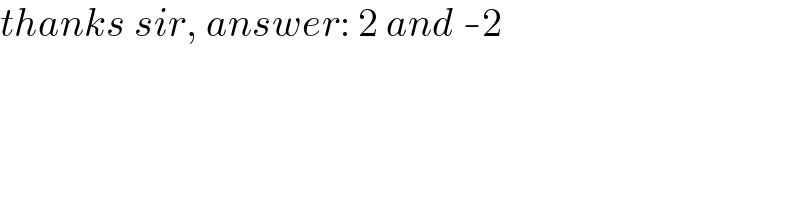
$${thanks}\:{sir},\:{answer}:\:\mathrm{2}\:{and}\:-\mathrm{2} \\ $$
Answered by Rasheed.Sindhi last updated on 24/Jun/21

$$\left(\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}\right)^{{z}} +\left(\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}\right)^{{z}} =\mathrm{10} \\ $$$${Let}\:\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}={a}\: \\ $$$$\frac{\mathrm{1}}{{a}}=\frac{\mathrm{1}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}=\frac{\mathrm{1}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}×\frac{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{25}−\mathrm{24}}=\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\left(\sqrt{{a}}\right)^{{z}} +\left(\sqrt{\frac{\mathrm{1}}{\:{a}}}\right)^{{z}} =\mathrm{10} \\ $$$$\left(\sqrt{{a}}\right)^{{z}} +\frac{\mathrm{1}}{\left(\sqrt{{a}}\right)^{{z}} }=\mathrm{10} \\ $$$$\left(\left(\sqrt{{a}}\right)^{{z}} \right)^{\mathrm{2}} −\mathrm{10}\left(\sqrt{{a}}\right)^{{z}} +\mathrm{1}=\mathrm{0} \\ $$$$\left(\sqrt{{a}}\right)^{{z}} =\frac{\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{4}}}{\mathrm{2}}=\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$$${a}^{{z}} =\left(\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{{z}} =\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} \:\vee\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{{z}} =\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} \\ $$$${z}=\mathrm{2}\:\vee\:\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{{z}} =\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{−\mathrm{2}} \\ $$$${z}=\mathrm{2}\:\vee\:{z}=−\mathrm{2} \\ $$
Commented by mathdanisur last updated on 24/Jun/21

$${Thanks}\:{Sir}\:{cool} \\ $$
