Menu Close

5-2x-1-5-2x-5-2x-5-2x-1-0-04-x-1-

Tinku Tara 0 Comments
Pin




Question Number 24839 by kosarrr last updated on 27/Nov/17
((5^(2x+1) +5^(2x) )/(5^(2x) +5^(2x−1) ))=(0/04)^(x−1)
$$\frac{\mathrm{5}^{\mathrm{2}{x}+\mathrm{1}} +\mathrm{5}^{\mathrm{2}{x}} }{\mathrm{5}^{\mathrm{2}{x}} +\mathrm{5}^{\mathrm{2}{x}−\mathrm{1}} }=\left(\mathrm{0}/\mathrm{04}\right)^{{x}−\mathrm{1}} \\ $$
Commented by behi.8.3.4.17@gmail.com last updated on 27/Nov/17
LHS=((5^(2x) (5+1))/(5^(2x) (1+(1/5))))=(6/(6/5))=5 ⇒5^1 =((4/(100)))^(x−1) =((1/(25)))^(x−1) =((1/5^2 ))^(x−1) =5^(−2(x−1)) ⇒1=−2(x−1)⇒−2x+2=1⇒−2x=−1 ⇒x=((−1)/(−2))=(1/2) ■
$$\boldsymbol{{LHS}}=\frac{\mathrm{5}^{\mathrm{2x}} \left(\mathrm{5}+\mathrm{1}\right)}{\mathrm{5}^{\mathrm{2x}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}\right)}=\frac{\mathrm{6}}{\frac{\mathrm{6}}{\mathrm{5}}}=\mathrm{5} \\ $$$$\Rightarrow\mathrm{5}^{\mathrm{1}} =\left(\frac{\mathrm{4}}{\mathrm{100}}\right)^{\mathrm{x}−\mathrm{1}} =\left(\frac{\mathrm{1}}{\mathrm{25}}\right)^{\mathrm{x}−\mathrm{1}} =\left(\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }\right)^{\mathrm{x}−\mathrm{1}} =\mathrm{5}^{−\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)} \\ $$$$\Rightarrow\mathrm{1}=−\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)\Rightarrow−\mathrm{2x}+\mathrm{2}=\mathrm{1}\Rightarrow−\mathrm{2x}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\frac{−\mathrm{1}}{−\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\blacksquare \\ $$
Answered by prakash jain last updated on 27/Nov/17
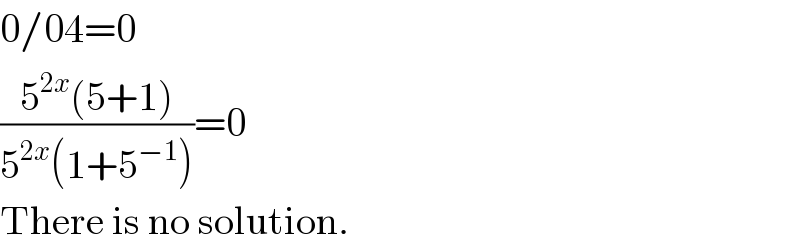
0/04=0 ((5^(2x) (5+1))/(5^(2x) (1+5^(−1) )))=0 There is no solution.
$$\mathrm{0}/\mathrm{04}=\mathrm{0} \\ $$$$\frac{\mathrm{5}^{\mathrm{2}{x}} \left(\mathrm{5}+\mathrm{1}\right)}{\mathrm{5}^{\mathrm{2}{x}} \left(\mathrm{1}+\mathrm{5}^{−\mathrm{1}} \right)}=\mathrm{0} \\ $$$$\mathrm{There}\:\mathrm{is}\:\mathrm{no}\:\mathrm{solution}. \\ $$
Answered by nnnavendu last updated on 27/Nov/17
ans. 5^(2x+1) +5^(2x) =0 5^(2x+1) =−5^(2x) squring both side (5^(2x+1) )^2 =(−5^(2x) )^2 5^(4x+2) =5^(4x) 4x+2=4x 4x−4x=−2 0x=−2 x=−(2/0) x=α(infinite)
$$\mathrm{ans}. \\ $$$$\mathrm{5}^{\mathrm{2x}+\mathrm{1}} +\mathrm{5}^{\mathrm{2x}} =\mathrm{0} \\ $$$$\mathrm{5}^{\mathrm{2x}+\mathrm{1}} =−\mathrm{5}^{\mathrm{2x}} \\ $$$$\mathrm{squring}\:\mathrm{both}\:\mathrm{side} \\ $$$$\left(\mathrm{5}^{\mathrm{2x}+\mathrm{1}} \right)^{\mathrm{2}} =\left(−\mathrm{5}^{\mathrm{2x}} \right)^{\mathrm{2}} \\ $$$$\mathrm{5}^{\mathrm{4x}+\mathrm{2}} =\mathrm{5}^{\mathrm{4x}} \\ $$$$\mathrm{4x}+\mathrm{2}=\mathrm{4x} \\ $$$$\mathrm{4x}−\mathrm{4x}=−\mathrm{2} \\ $$$$\mathrm{0x}=−\mathrm{2} \\ $$$$\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{0}} \\ $$$$\mathrm{x}=\alpha\left(\mathrm{infinite}\right) \\ $$
Commented by prakash jain last updated on 27/Nov/17
x=∞ will bring LHS to (∞/∞) form. So infinity is not a valid answer. lim_(x→∞) ((5^(2x+1) +5^(2x) )/(5^(2x) +5^(2x−1) )) lim_(x→∞) ((5^(2x) (5+1))/(5^(2x) (1+5^(−1) ))) lim_(x→∞) (6/(6/5))=5
$${x}=\infty\:\mathrm{will}\:\mathrm{bring}\:\mathrm{LHS}\:\mathrm{to} \\ $$$$\frac{\infty}{\infty}\:\mathrm{form}.\:\mathrm{So}\:\mathrm{infinity}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{valid} \\ $$$$\mathrm{answer}. \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}^{\mathrm{2}{x}+\mathrm{1}} +\mathrm{5}^{\mathrm{2}{x}} }{\mathrm{5}^{\mathrm{2}{x}} +\mathrm{5}^{\mathrm{2}{x}−\mathrm{1}} } \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}^{\mathrm{2}{x}} \left(\mathrm{5}+\mathrm{1}\right)}{\mathrm{5}^{\mathrm{2}{x}} \left(\mathrm{1}+\mathrm{5}^{−\mathrm{1}} \right)} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{6}}{\mathrm{6}/\mathrm{5}}=\mathrm{5} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *