Question Number 154255 by EDWIN88 last updated on 16/Sep/21
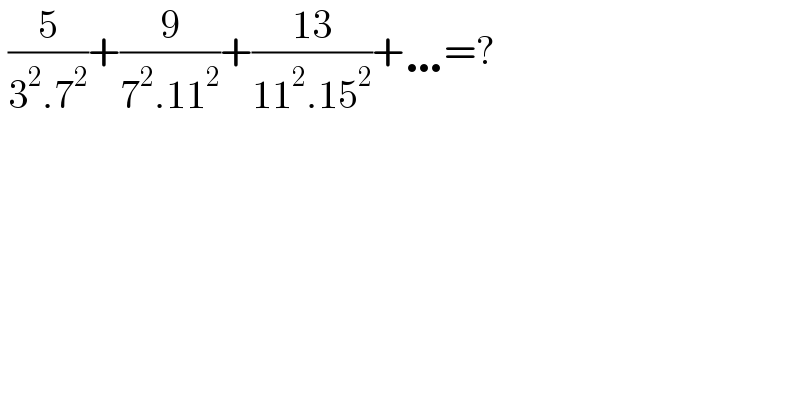
$$\:\frac{\mathrm{5}}{\mathrm{3}^{\mathrm{2}} .\mathrm{7}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{7}^{\mathrm{2}} .\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{13}}{\mathrm{11}^{\mathrm{2}} .\mathrm{15}^{\mathrm{2}} }+\ldots=? \\ $$
Answered by ARUNG_Brandon_MBU last updated on 16/Sep/21

$${S}=\frac{\mathrm{5}}{\mathrm{3}^{\mathrm{2}} .\mathrm{7}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{7}^{\mathrm{2}} .\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{13}}{\mathrm{11}^{\mathrm{2}} .\mathrm{15}^{\mathrm{2}} }+\ldots \\ $$$$\:\:\:=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{4}{n}+\mathrm{1}}{\left(\mathrm{4}{n}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{4}{n}+\mathrm{3}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{\left(\mathrm{4}{n}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{4}{n}+\mathrm{3}\right)^{\mathrm{2}} }\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{15}^{\mathrm{2}} }+\centerdot\centerdot\centerdot\right)=\frac{\mathrm{1}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{72}} \\ $$
