Question Number 57368 by problem solverd last updated on 03/Apr/19
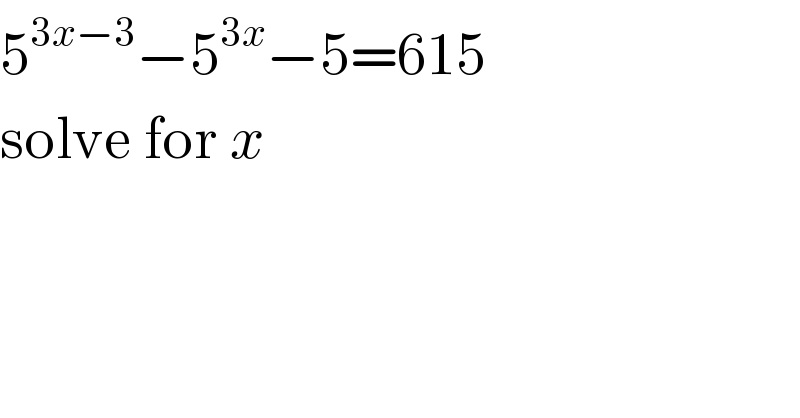
$$\mathrm{5}^{\mathrm{3}{x}−\mathrm{3}} −\mathrm{5}^{\mathrm{3}{x}} −\mathrm{5}=\mathrm{615} \\ $$$$\mathrm{solve}\:\mathrm{for}\:{x} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Apr/19

$$\mathrm{5}^{\mathrm{3}{x}} ={a} \\ $$$$\frac{\mathrm{5}^{\mathrm{3}{x}} }{\mathrm{5}^{\mathrm{3}} }−\mathrm{5}^{\mathrm{3}{x}} −\mathrm{5}=\mathrm{615} \\ $$$$\frac{{a}}{\mathrm{125}}−{a}=\mathrm{620} \\ $$$$\frac{{a}−\mathrm{125}{a}}{\mathrm{125}}=\mathrm{620} \\ $$$$−\mathrm{124}{a}=\mathrm{620}×\mathrm{125} \\ $$$${a}=\frac{−\mathrm{620}×\mathrm{125}}{\mathrm{124}}=\frac{−\mathrm{5}×\mathrm{125}}{\mathrm{1}}=−\mathrm{5}^{\mathrm{4}} \\ $$$$\mathrm{5}^{\mathrm{3}{x}} =−\mathrm{5}^{\mathrm{4}} \\ $$$${here}\:{is}\:{the}\:{problem}\:{arises}.. \\ $$$$\mathrm{5}^{\mathrm{3}{x}} \:{can}\:{not}\:{be}\:{negetive}… \\ $$$$ \\ $$
Commented by MJS last updated on 04/Apr/19
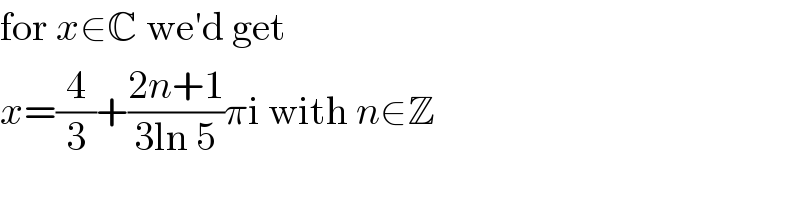
$$\mathrm{for}\:{x}\in\mathbb{C}\:\mathrm{we}'\mathrm{d}\:\mathrm{get} \\ $$$${x}=\frac{\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{3ln}\:\mathrm{5}}\pi\mathrm{i}\:\mathrm{with}\:{n}\in\mathbb{Z} \\ $$
