Menu Close

5-4-1-2-m-n-m-n-

Tinku Tara 0 Comments
Pin




Question Number 173798 by payamnazerian last updated on 18/Jul/22
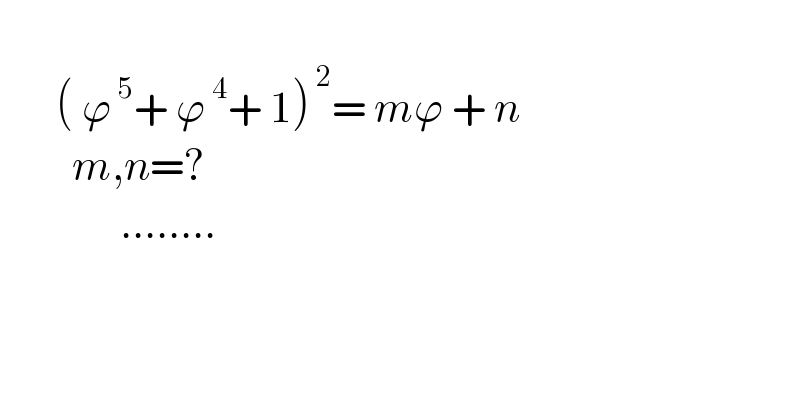
( ϕ^( 5) + ϕ^( 4) + 1)^( 2) = mϕ + n m,n=? ........
$$ \\ $$$$\:\:\:\:\:\:\:\left(\:\varphi^{\:\mathrm{5}} +\:\varphi^{\:\mathrm{4}} +\:\mathrm{1}\right)^{\:\mathrm{2}} =\:{m}\varphi\:+\:{n} \\ $$$$\:\:\:\:\:\:\:\:\:{m},{n}=? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…….. \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$
Answered by mr W last updated on 18/Jul/22
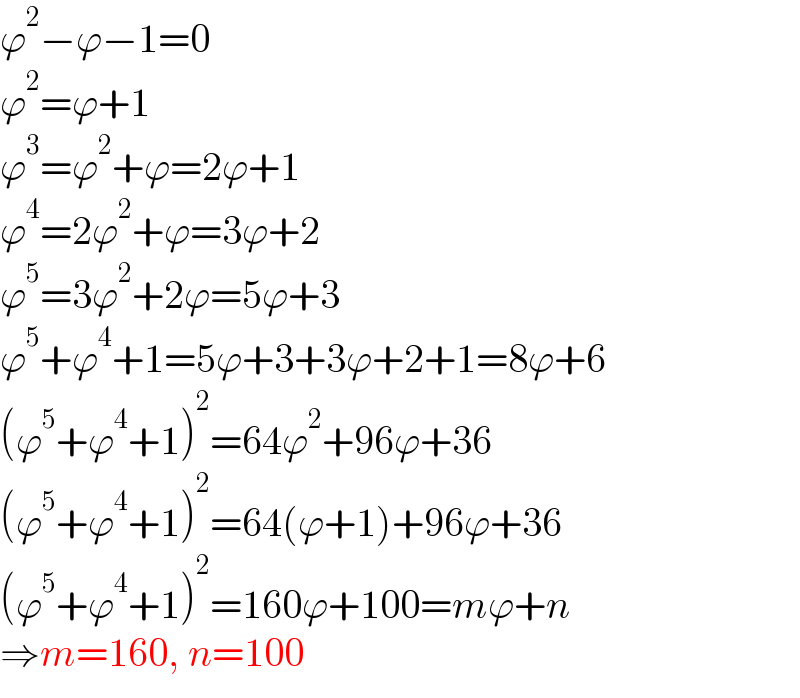
ϕ^2 −ϕ−1=0 ϕ^2 =ϕ+1 ϕ^3 =ϕ^2 +ϕ=2ϕ+1 ϕ^4 =2ϕ^2 +ϕ=3ϕ+2 ϕ^5 =3ϕ^2 +2ϕ=5ϕ+3 ϕ^5 +ϕ^4 +1=5ϕ+3+3ϕ+2+1=8ϕ+6 (ϕ^5 +ϕ^4 +1)^2 =64ϕ^2 +96ϕ+36 (ϕ^5 +ϕ^4 +1)^2 =64(ϕ+1)+96ϕ+36 (ϕ^5 +ϕ^4 +1)^2 =160ϕ+100=mϕ+n ⇒m=160, n=100
$$\varphi^{\mathrm{2}} −\varphi−\mathrm{1}=\mathrm{0} \\ $$$$\varphi^{\mathrm{2}} =\varphi+\mathrm{1} \\ $$$$\varphi^{\mathrm{3}} =\varphi^{\mathrm{2}} +\varphi=\mathrm{2}\varphi+\mathrm{1} \\ $$$$\varphi^{\mathrm{4}} =\mathrm{2}\varphi^{\mathrm{2}} +\varphi=\mathrm{3}\varphi+\mathrm{2} \\ $$$$\varphi^{\mathrm{5}} =\mathrm{3}\varphi^{\mathrm{2}} +\mathrm{2}\varphi=\mathrm{5}\varphi+\mathrm{3} \\ $$$$\varphi^{\mathrm{5}} +\varphi^{\mathrm{4}} +\mathrm{1}=\mathrm{5}\varphi+\mathrm{3}+\mathrm{3}\varphi+\mathrm{2}+\mathrm{1}=\mathrm{8}\varphi+\mathrm{6} \\ $$$$\left(\varphi^{\mathrm{5}} +\varphi^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{64}\varphi^{\mathrm{2}} +\mathrm{96}\varphi+\mathrm{36} \\ $$$$\left(\varphi^{\mathrm{5}} +\varphi^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{64}\left(\varphi+\mathrm{1}\right)+\mathrm{96}\varphi+\mathrm{36} \\ $$$$\left(\varphi^{\mathrm{5}} +\varphi^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{160}\varphi+\mathrm{100}={m}\varphi+{n} \\ $$$$\Rightarrow{m}=\mathrm{160},\:{n}=\mathrm{100} \\ $$
Commented by Tawa11 last updated on 18/Jul/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mnjuly1970 last updated on 18/Jul/22
grateful sir
$$\:\:\:\:{grateful}\:{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Jul/22
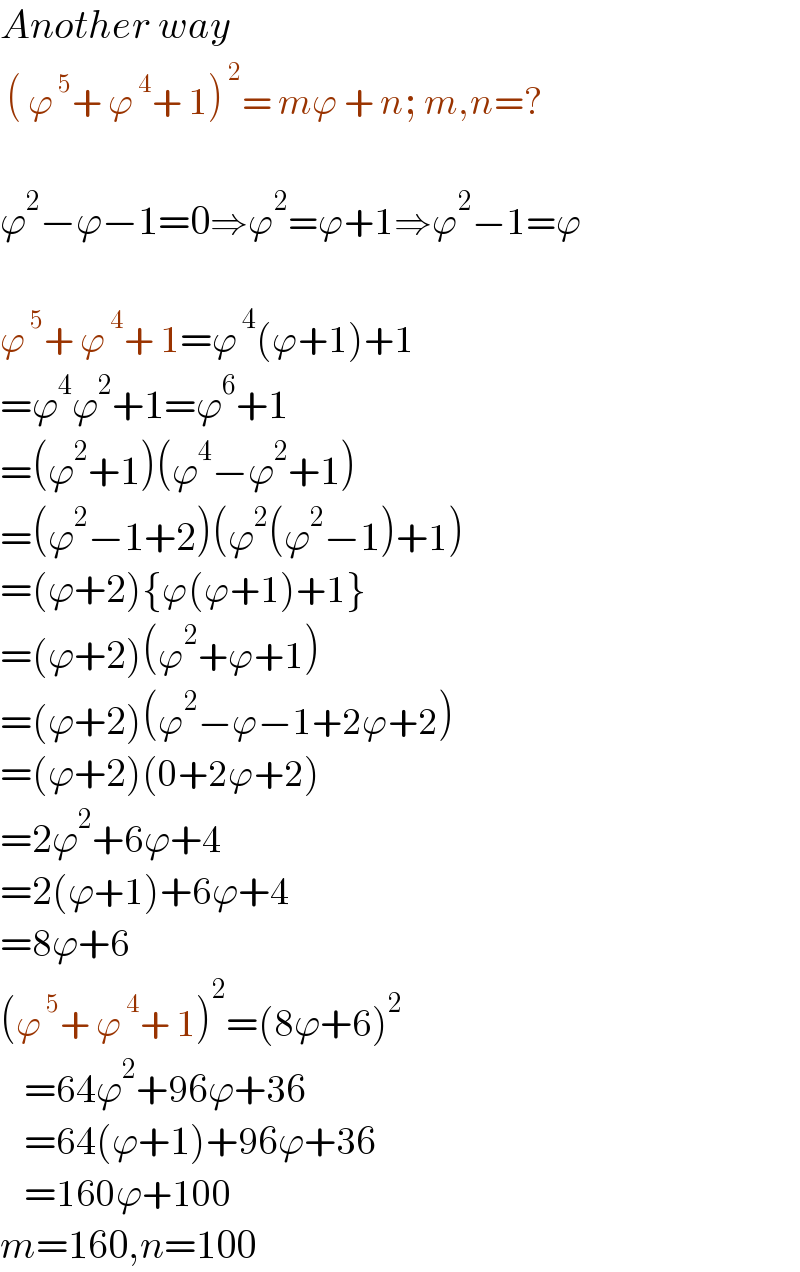
Another way ( ϕ^( 5) + ϕ^( 4) + 1)^( 2) = mϕ + n; m,n=? ϕ^2 −ϕ−1=0⇒ϕ^2 =ϕ+1⇒ϕ^2 −1=ϕ ϕ^( 5) + ϕ^( 4) + 1=ϕ^( 4) (ϕ+1)+1 =ϕ^4 ϕ^2 +1=ϕ^6 +1 =(ϕ^2 +1)(ϕ^4 −ϕ^2 +1) =(ϕ^2 −1+2)(ϕ^2 (ϕ^2 −1)+1) =(ϕ+2){ϕ(ϕ+1)+1} =(ϕ+2)(ϕ^2 +ϕ+1) =(ϕ+2)(ϕ^2 −ϕ−1+2ϕ+2) =(ϕ+2)(0+2ϕ+2) =2ϕ^2 +6ϕ+4 =2(ϕ+1)+6ϕ+4 =8ϕ+6 (ϕ^( 5) + ϕ^( 4) + 1)^2 =(8ϕ+6)^2 =64ϕ^2 +96ϕ+36 =64(ϕ+1)+96ϕ+36 =160ϕ+100 m=160,n=100
$${Another}\:{way} \\ $$$$\:\left(\:\varphi^{\:\mathrm{5}} +\:\varphi^{\:\mathrm{4}} +\:\mathrm{1}\right)^{\:\mathrm{2}} =\:{m}\varphi\:+\:{n};\:{m},{n}=? \\ $$$$ \\ $$$$\varphi^{\mathrm{2}} −\varphi−\mathrm{1}=\mathrm{0}\Rightarrow\varphi^{\mathrm{2}} =\varphi+\mathrm{1}\Rightarrow\varphi^{\mathrm{2}} −\mathrm{1}=\varphi \\ $$$$ \\ $$$$\varphi^{\:\mathrm{5}} +\:\varphi^{\:\mathrm{4}} +\:\mathrm{1}=\varphi^{\:\mathrm{4}} \left(\varphi+\mathrm{1}\right)+\mathrm{1} \\ $$$$=\varphi^{\mathrm{4}} \varphi^{\mathrm{2}} +\mathrm{1}=\varphi^{\mathrm{6}} +\mathrm{1} \\ $$$$=\left(\varphi^{\mathrm{2}} +\mathrm{1}\right)\left(\varphi^{\mathrm{4}} −\varphi^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$=\left(\varphi^{\mathrm{2}} −\mathrm{1}+\mathrm{2}\right)\left(\varphi^{\mathrm{2}} \left(\varphi^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{1}\right) \\ $$$$=\left(\varphi+\mathrm{2}\right)\left\{\varphi\left(\varphi+\mathrm{1}\right)+\mathrm{1}\right\} \\ $$$$=\left(\varphi+\mathrm{2}\right)\left(\varphi^{\mathrm{2}} +\varphi+\mathrm{1}\right) \\ $$$$=\left(\varphi+\mathrm{2}\right)\left(\varphi^{\mathrm{2}} −\varphi−\mathrm{1}+\mathrm{2}\varphi+\mathrm{2}\right) \\ $$$$=\left(\varphi+\mathrm{2}\right)\left(\mathrm{0}+\mathrm{2}\varphi+\mathrm{2}\right) \\ $$$$=\mathrm{2}\varphi^{\mathrm{2}} +\mathrm{6}\varphi+\mathrm{4} \\ $$$$=\mathrm{2}\left(\varphi+\mathrm{1}\right)+\mathrm{6}\varphi+\mathrm{4} \\ $$$$=\mathrm{8}\varphi+\mathrm{6} \\ $$$$\left(\varphi^{\:\mathrm{5}} +\:\varphi^{\:\mathrm{4}} +\:\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{8}\varphi+\mathrm{6}\right)^{\mathrm{2}} \\ $$$$\:\:\:=\mathrm{64}\varphi^{\mathrm{2}} +\mathrm{96}\varphi+\mathrm{36} \\ $$$$\:\:\:=\mathrm{64}\left(\varphi+\mathrm{1}\right)+\mathrm{96}\varphi+\mathrm{36} \\ $$$$\:\:\:=\mathrm{160}\varphi+\mathrm{100} \\ $$$${m}=\mathrm{160},{n}=\mathrm{100} \\ $$
Commented by mnjuly1970 last updated on 19/Jul/22
thanks alot sir
$$\:\:{thanks}\:{alot}\:{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Jul/22
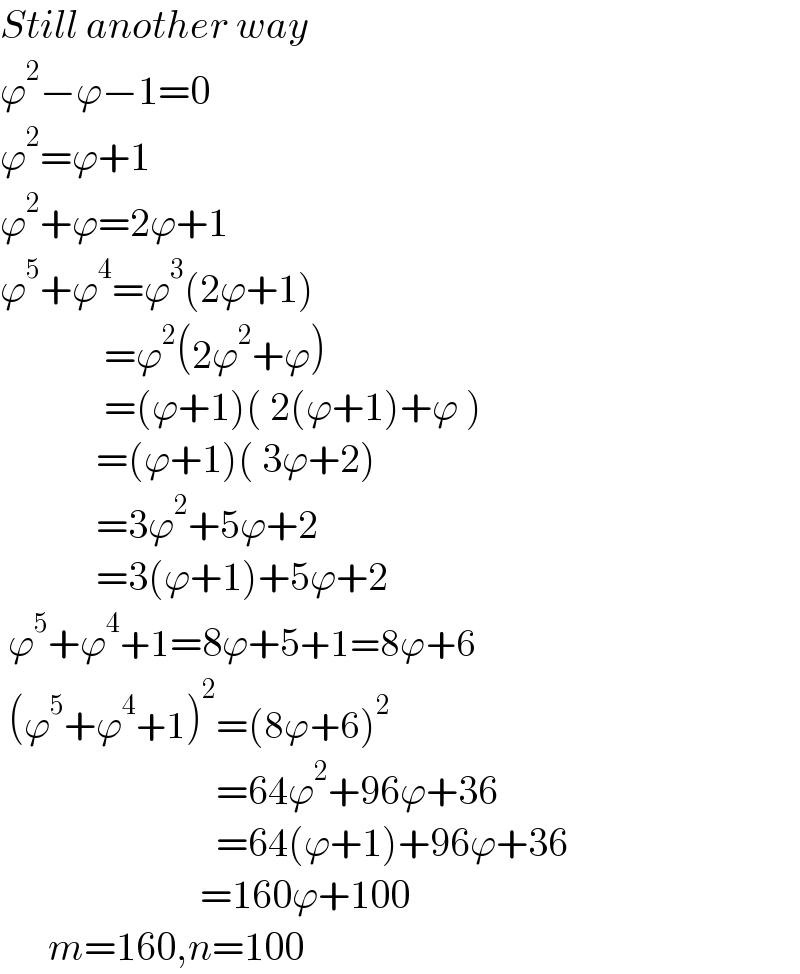
Still another way ϕ^2 −ϕ−1=0 ϕ^2 =ϕ+1 ϕ^2 +ϕ=2ϕ+1 ϕ^5 +ϕ^4 =ϕ^3 (2ϕ+1) =ϕ^2 (2ϕ^2 +ϕ) =(ϕ+1)( 2(ϕ+1)+ϕ ) =(ϕ+1)( 3ϕ+2) =3ϕ^2 +5ϕ+2 =3(ϕ+1)+5ϕ+2 ϕ^5 +ϕ^4 +1=8ϕ+5+1=8ϕ+6 (ϕ^5 +ϕ^4 +1)^2 =(8ϕ+6)^2 =64ϕ^2 +96ϕ+36 =64(ϕ+1)+96ϕ+36 =160ϕ+100 m=160,n=100
$${Still}\:{another}\:{way} \\ $$$$\varphi^{\mathrm{2}} −\varphi−\mathrm{1}=\mathrm{0} \\ $$$$\varphi^{\mathrm{2}} =\varphi+\mathrm{1} \\ $$$$\varphi^{\mathrm{2}} +\varphi=\mathrm{2}\varphi+\mathrm{1} \\ $$$$\varphi^{\mathrm{5}} +\varphi^{\mathrm{4}} =\varphi^{\mathrm{3}} \left(\mathrm{2}\varphi+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\varphi^{\mathrm{2}} \left(\mathrm{2}\varphi^{\mathrm{2}} +\varphi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\varphi+\mathrm{1}\right)\left(\:\mathrm{2}\left(\varphi+\mathrm{1}\right)+\varphi\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left(\varphi+\mathrm{1}\right)\left(\:\mathrm{3}\varphi+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}\varphi^{\mathrm{2}} +\mathrm{5}\varphi+\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}\left(\varphi+\mathrm{1}\right)+\mathrm{5}\varphi+\mathrm{2} \\ $$$$\:\varphi^{\mathrm{5}} +\varphi^{\mathrm{4}} +\mathrm{1}=\mathrm{8}\varphi+\mathrm{5}+\mathrm{1}=\mathrm{8}\varphi+\mathrm{6} \\ $$$$\:\left(\varphi^{\mathrm{5}} +\varphi^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{8}\varphi+\mathrm{6}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{64}\varphi^{\mathrm{2}} +\mathrm{96}\varphi+\mathrm{36} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{64}\left(\varphi+\mathrm{1}\right)+\mathrm{96}\varphi+\mathrm{36} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{160}\varphi+\mathrm{100} \\ $$$$\:\:\:\:\:\:{m}=\mathrm{160},{n}=\mathrm{100} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *