Question Number 151300 by mathdanisur last updated on 19/Aug/21
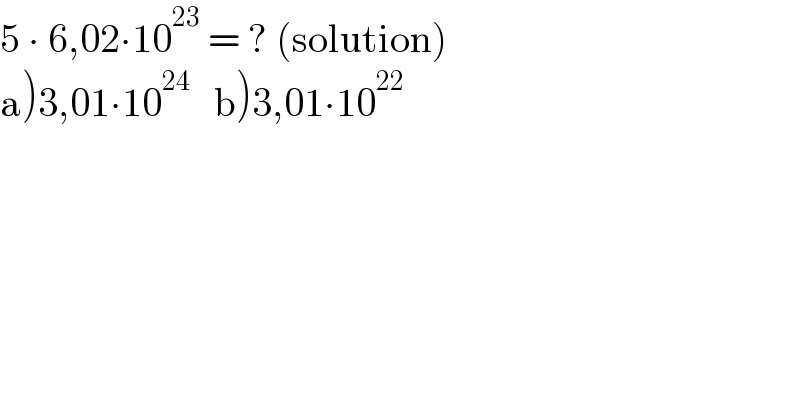
$$\mathrm{5}\:\centerdot\:\mathrm{6},\mathrm{02}\centerdot\mathrm{10}^{\mathrm{23}} \:=\:?\:\left(\mathrm{solution}\right) \\ $$$$\left.\mathrm{a}\left.\right)\mathrm{3},\mathrm{01}\centerdot\mathrm{10}^{\mathrm{24}} \:\:\:\mathrm{b}\right)\mathrm{3},\mathrm{01}\centerdot\mathrm{10}^{\mathrm{22}} \\ $$
Answered by puissant last updated on 19/Aug/21

$$\mathrm{5}×\mathrm{6},\mathrm{02}.\mathrm{10}^{\mathrm{23}} =\mathrm{3},\mathrm{1}.\mathrm{10}^{\mathrm{24}} .. \\ $$$$\left.{a}\right) \\ $$
Answered by amin96 last updated on 19/Aug/21
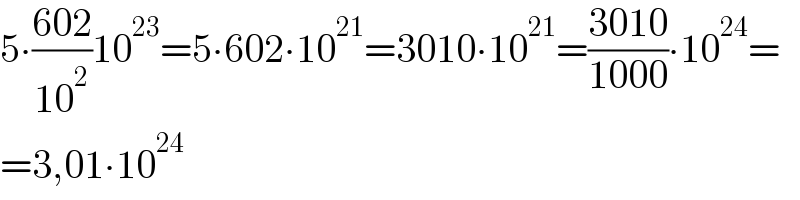
$$\mathrm{5}\centerdot\frac{\mathrm{602}}{\mathrm{10}^{\mathrm{2}} }\mathrm{10}^{\mathrm{23}} =\mathrm{5}\centerdot\mathrm{602}\centerdot\mathrm{10}^{\mathrm{21}} =\mathrm{3010}\centerdot\mathrm{10}^{\mathrm{21}} =\frac{\mathrm{3010}}{\mathrm{1000}}\centerdot\mathrm{10}^{\mathrm{24}} = \\ $$$$=\mathrm{3},\mathrm{01}\centerdot\mathrm{10}^{\mathrm{24}} \\ $$
Commented by mathdanisur last updated on 20/Aug/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
Answered by Olaf_Thorendsen last updated on 19/Aug/21

$$\mathrm{5}×\mathrm{6},\mathrm{02}.\mathrm{10}^{\mathrm{23}} \:=\:\mathrm{5}\mathscr{N}\:=\:\mathrm{5}\:\mathrm{moles}\:\left(\mathrm{lol}\:!\right) \\ $$
