Question Number 115246 by bemath last updated on 24/Sep/20

$$\:\:\:\:\mathrm{5}^{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \:+\:\mathrm{625}\:\leqslant\:\mathrm{5}^{{x}^{\mathrm{2}} +\mathrm{2}} \:+\:\mathrm{5}^{\mathrm{2}{x}+\mathrm{3}} \\ $$
Commented by bobhans last updated on 24/Sep/20
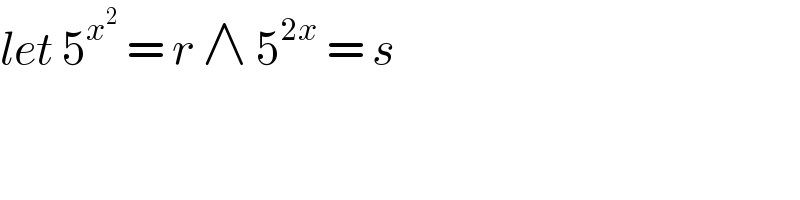
$${let}\:\mathrm{5}^{{x}^{\mathrm{2}} } \:=\:{r}\:\wedge\:\mathrm{5}^{\mathrm{2}{x}} \:=\:{s} \\ $$
