Question Number 92448 by jagoll last updated on 07/May/20

$$\begin{cases}{\mathrm{5}^{\mathrm{x}} .\mathrm{6}^{\mathrm{y}} \:=\:\mathrm{150}}\\{\mathrm{5}^{\mathrm{y}} .\mathrm{6}^{\mathrm{x}} \:=\:\mathrm{180}\:}\end{cases} \\ $$
Commented by john santu last updated on 07/May/20
����������
Answered by john santu last updated on 07/May/20
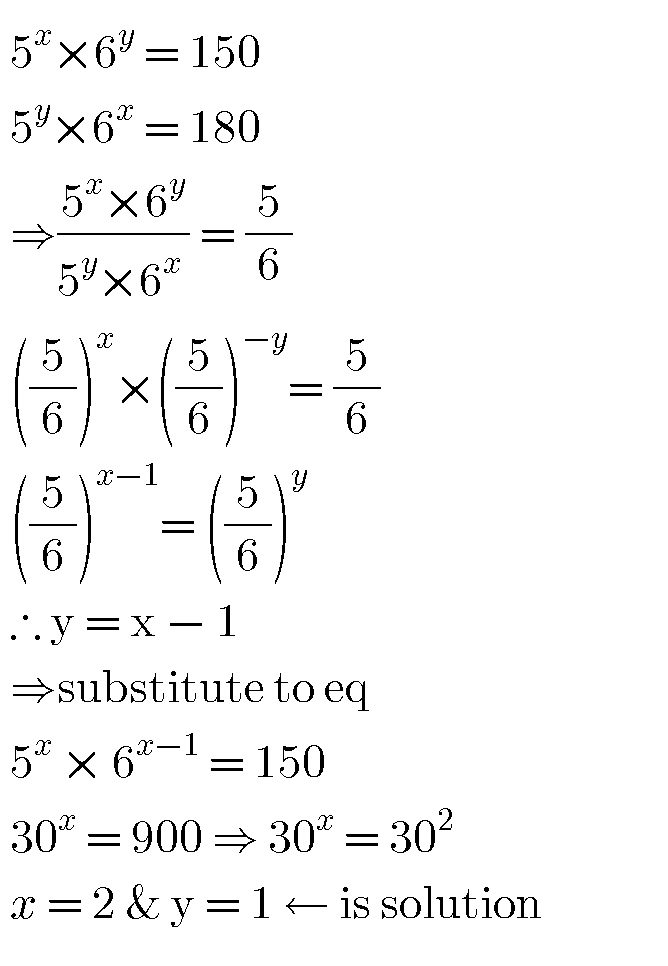
Commented by jagoll last updated on 07/May/20
☺☺��
Answered by $@ty@m123 last updated on 07/May/20
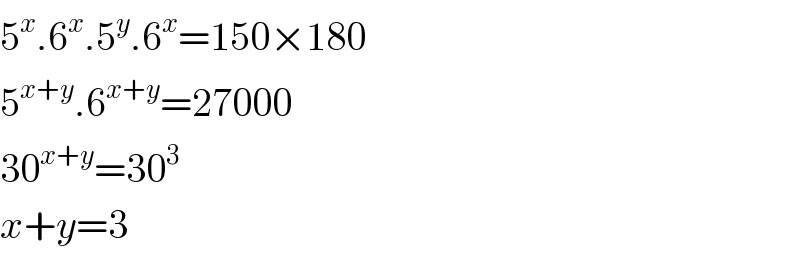
$$\mathrm{5}^{{x}} .\mathrm{6}^{{x}} .\mathrm{5}^{{y}} .\mathrm{6}^{{x}} =\mathrm{150}×\mathrm{180} \\ $$$$\mathrm{5}^{{x}+{y}} .\mathrm{6}^{{x}+{y}} =\mathrm{27000} \\ $$$$\mathrm{30}^{{x}+{y}} =\mathrm{30}^{\mathrm{3}} \\ $$$${x}+{y}=\mathrm{3} \\ $$
Commented by jagoll last updated on 07/May/20
��
Answered by Rasheed.Sindhi last updated on 07/May/20
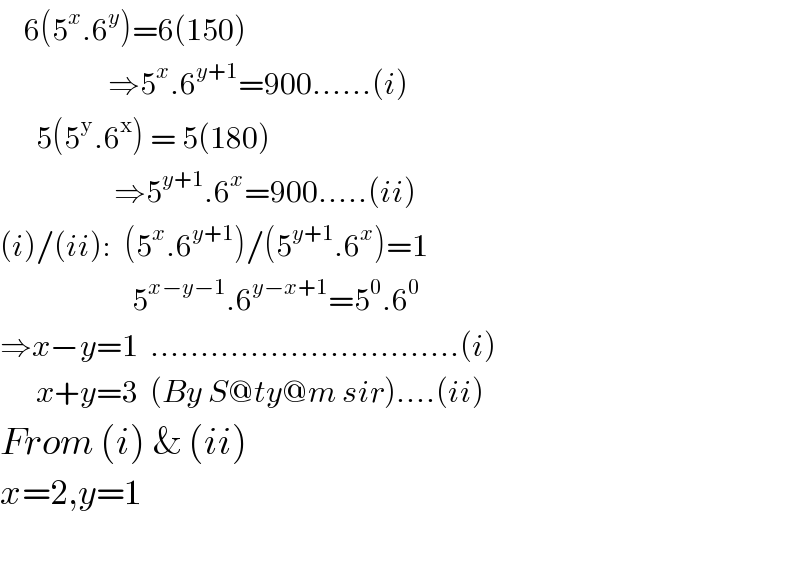
$$\:\:\:\:\mathrm{6}\left(\mathrm{5}^{{x}} .\mathrm{6}^{{y}} \right)=\mathrm{6}\left(\mathrm{150}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{5}^{{x}} .\mathrm{6}^{{y}+\mathrm{1}} =\mathrm{900}……\left({i}\right) \\ $$$$\:\:\:\:\:\:\mathrm{5}\left(\mathrm{5}^{\mathrm{y}} .\mathrm{6}^{\mathrm{x}} \right)\:=\:\mathrm{5}\left(\mathrm{180}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{5}^{{y}+\mathrm{1}} .\mathrm{6}^{{x}} =\mathrm{900}…..\left({ii}\right) \\ $$$$\left({i}\right)/\left({ii}\right):\:\:\left(\mathrm{5}^{{x}} .\mathrm{6}^{{y}+\mathrm{1}} \right)/\left(\mathrm{5}^{{y}+\mathrm{1}} .\mathrm{6}^{{x}} \right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}^{{x}−{y}−\mathrm{1}} .\mathrm{6}^{{y}−{x}+\mathrm{1}} =\mathrm{5}^{\mathrm{0}} .\mathrm{6}^{\mathrm{0}} \\ $$$$\Rightarrow{x}−{y}=\mathrm{1}\:\:………………………….\left({i}\right) \\ $$$$\:\:\:\:\:\:{x}+{y}=\mathrm{3}\:\:\left({By}\:{S}@{ty}@{m}\:{sir}\right)….\left({ii}\right)\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${From}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$${x}=\mathrm{2},{y}=\mathrm{1} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 07/May/20

$${By}\:{Factorization} \\ $$$$\mathrm{150}\:{and}\:\mathrm{180}\:{can}\:{be}\:{written}\:{as}\: \\ $$$${product}\:{of}\:\mathrm{5}\:\&\:\mathrm{6}: \\ $$$$\:\begin{cases}{\mathrm{5}^{{x}} .\mathrm{6}^{{y}} =\mathrm{150}=\mathrm{2}.\mathrm{3}.\mathrm{5}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} .\mathrm{6}^{\mathrm{1}} }\\{\mathrm{5}^{{y}} .\mathrm{6}^{{x}} =\mathrm{180}=\mathrm{2}^{\mathrm{2}} .\mathrm{3}^{\mathrm{2}} .\mathrm{5}=\mathrm{5}^{\mathrm{1}} .\mathrm{6}^{\mathrm{2}} }\end{cases} \\ $$$$\Rightarrow{x}=\mathrm{2}\:\wedge\:{y}=\mathrm{1} \\ $$
Commented by Prithwish Sen 1 last updated on 08/May/20

$$\mathrm{wow}! \\ $$
Commented by Rasheed.Sindhi last updated on 08/May/20

$$\mathcal{T}{h}\alpha{n}\mathcal{X}\:{sir}. \\ $$$${Moreover}: \\ $$$${If}\:{in}\:{an}\:{equation}\:{a}^{{x}} .{b}^{{y}} ={c},\:\:{c}\:{can}\:{be} \\ $$$${written}\:{as}\:{a}\:{product}\:{of}\:{a}\:\&\:{b}\:{in} \\ $$$${a}\:\boldsymbol{{unique}}\:{way}\:\left({as}\:{in}\:{this}\:{case}\right)\:{only} \\ $$$${one}\:{equation}\:{is}\:{sufficient}! \\ $$
Commented by Prithwish Sen 1 last updated on 08/May/20

$$\mathrm{agree} \\ $$
