Question Number 97531 by 281981 last updated on 08/Jun/20
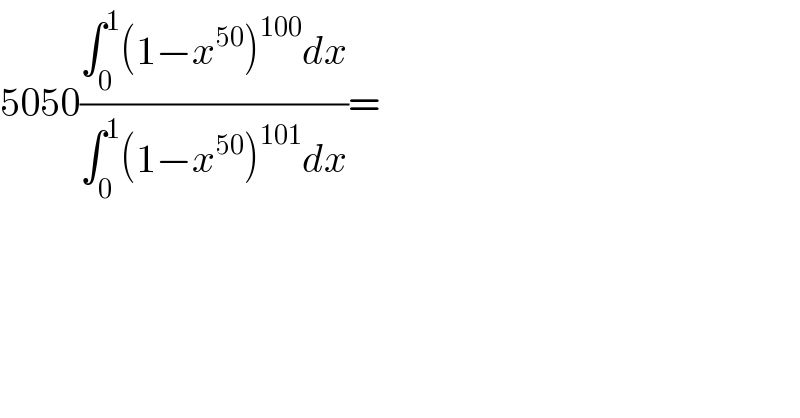
$$\mathrm{5050}\frac{\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{50}} \right)^{\mathrm{100}} {dx}}{\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{50}} \right)^{\mathrm{101}} {dx}}= \\ $$
Answered by smridha last updated on 08/Jun/20

$$\boldsymbol{{let}}\:\left(\mathrm{1}−\boldsymbol{{x}}^{\mathrm{50}} \right)=\boldsymbol{{m}}\:{so}\:{x}=\left(\mathrm{1}−{m}\right)^{\frac{\mathrm{1}}{\mathrm{50}}} \\ $$$${now}, \\ $$$$\mathrm{5050}\frac{\frac{\mathrm{1}}{\mathrm{50}}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{m}}^{\left(\mathrm{101}−\mathrm{1}\right)} \left(\mathrm{1}−\boldsymbol{{m}}\right)^{\frac{\mathrm{1}}{\mathrm{50}}−\mathrm{1}} \boldsymbol{{dm}}}{\frac{\mathrm{1}}{\mathrm{50}}\int_{\mathrm{0}} ^{\mathrm{1}} \left({m}\right)^{\left(\mathrm{102}−\mathrm{1}\right)} \left(\mathrm{1}−{m}\right)^{\frac{\mathrm{1}}{\mathrm{50}}−\mathrm{1}} \boldsymbol{{dm}}} \\ $$$$=\mathrm{5050}\frac{\frac{\Gamma\left(\mathrm{101}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{50}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{101}+\frac{\mathrm{1}}{\mathrm{50}}\right)}}{\frac{\Gamma\left(\mathrm{102}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{50}}\right)}{\Gamma\left(\mathrm{102}+\frac{\mathrm{1}}{\mathrm{50}}\right)}}=\mathrm{5050}\frac{\left(\mathrm{101}+\frac{\mathrm{1}}{\mathrm{50}}\right)}{\mathrm{101}} \\ $$$$=\mathrm{5051} \\ $$
Commented by 281981 last updated on 10/Jun/20
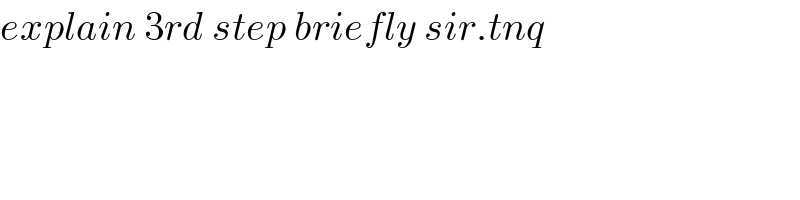
$${explain}\:\mathrm{3}{rd}\:{step}\:{briefly}\:{sir}.{tnq} \\ $$
Commented by smridha last updated on 10/Jun/20
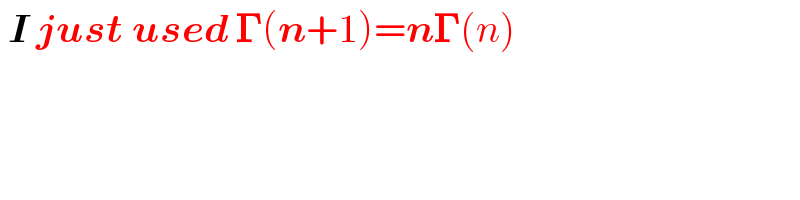
$$\:\boldsymbol{{I}}\:\boldsymbol{{just}}\:\boldsymbol{{used}}\:\boldsymbol{\Gamma}\left(\boldsymbol{{n}}+\mathrm{1}\right)=\boldsymbol{{n}\Gamma}\left({n}\right) \\ $$
Commented by smridha last updated on 10/Jun/20

$$\Gamma\left(\mathrm{102}+\frac{\mathrm{1}}{\mathrm{50}}\right)=\left(\mathrm{101}+\frac{\mathrm{1}}{\mathrm{50}}\right)\boldsymbol{\Gamma}\left(\mathrm{101}+\frac{\mathrm{1}}{\mathrm{50}}\right) \\ $$
