51b2cd-is-a-six-digit-perfect-square-that-is-divisible-by-both-5-and-11-What-is-the-sum-of-all-possible-values-of-it-

Question Number 160091 by abdullah_ff last updated on 24/Nov/21

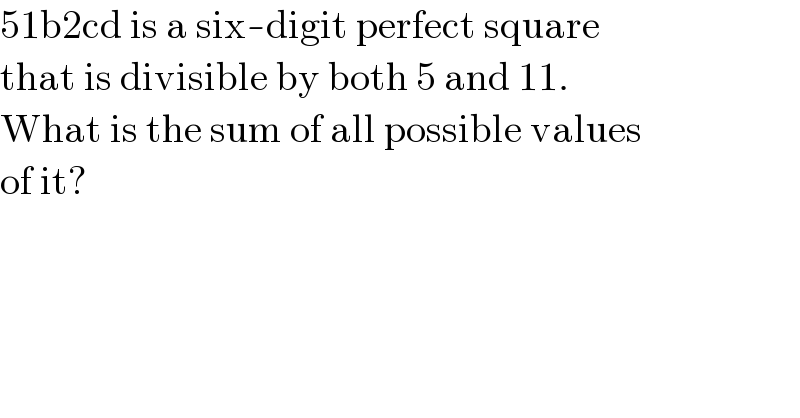
51 b 2 cd is a six - digit perfect square

that is divisible by both 5 and 11 .

What is the sum of all possible values

of it ?

Commented by Rasheed.Sindhi last updated on 24/Nov/21

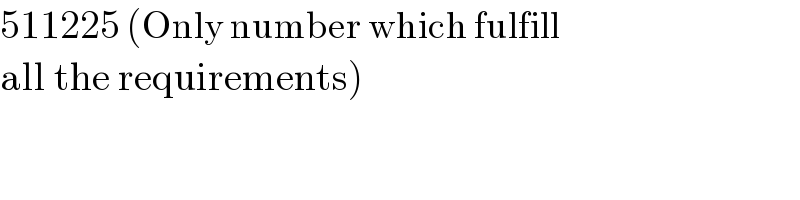
511225 (Only number which fulfill

all the requirements)

Answered by Rasheed.Sindhi last updated on 24/Nov/21

▸ 5 ∣ 51 b 2 cd \land 11 ∣ 51 b 2 cd

\land (51 b 2 cd is perfect - square)

\Rightarrow 25 ∣ 51 b 2 cd \land 121 ∣ 51 b 2 cd

\Rightarrow 25 \times 121 = 3025 ∣ 51 b 2 cd

\Rightarrow {3025 m}^{2} = 51 b 2 cd

m should be replaced so that {3025 m}^{2}

has leading two digits^{'} 51^{'} and 4 th

digit from left is 2 . So m = 13

3025 \times 13^{2} = 511225 .

No other number can fulfill all these

requirements .

Sum of all possible such numbers

= 511225 (∵ {there}^{'} s only single number)

Commented by abdullah_ff last updated on 24/Nov/21

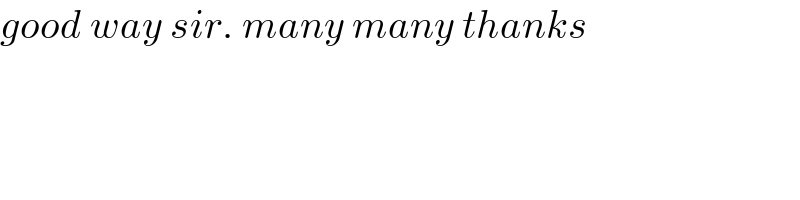
g o o d w a y s i r . m a n y m a n y t h a n k s

Answered by mr W last updated on 25/Nov/21

l e t 51 b 2 c d = n^{2}

510200 ⩽ n^{2} ⩽ 519299

\sqrt{510200} ⩽ n ⩽ \sqrt{519299}

\Rightarrow 715 ⩽ n ⩽ 720

s i n c e t h e n u m b e r i s d i v i s i b l e b y 5,

t h e l a s t d i g i t o f n^{2} m u s t b e 5 o r 0 .

t h e r e a r e o n l y t w o p o s s i b i l i t i e s :

n = 715 o r 720

\underset{―}{w i t h n = 715 :}

715^{2} = 511225 \equiv 0 m o d 11 (✓)

\underset{―}{w i t h n = 720 :}

720^{2} = 518400 ≢ 0 m o d 11 (\times)

s o w e h a v e o n l y 511225 a s s o l u t i o n .

Commented by abdullah_ff last updated on 25/Nov/21

t h a n k y o u v e r y m u c h s i r .

Commented by Rasheed.Sindhi last updated on 25/Nov/21

More efficient approach!

Answered by Rasheed.Sindhi last updated on 25/Nov/21

▸

∵ 51 b 2 cd is perfect square & 5 ∣ 51 b 2 cd

∴ 25 ∣ 51 b 2 cd

∴ cd = 00 \lor cd = 25

(xxxx 50 and xxxx 75 {aren}^{'} t perfect squares)

cd = 00 \Rightarrow 51 b 2 cd = 51 b 200 = 51 b 2 \times 100

\Rightarrow 51 b 2 shoud be perfect square but

it {can}^{'} t be due to 2 at unit place .

∴ cd = 00 (\times) & cd = 25 (✓)

▸

11 ∣ 51 b 2 cd \Rightarrow (5 + b + c) - (1 + 2 + d) = 0, 11 \dots

\Rightarrow (5 + b + 2) - (1 + 2 + 5) = 0, 11, \dots

\Rightarrow b - 1 = 0, 11 \Rightarrow b = 1, 12, \dots

∵ b is decimal digit ∴ b = 1

∴ 51 b 2 cd = 511225

Commented by abdullah_ff last updated on 25/Nov/21

t h a n k s!