Question Number 95920 by bobhans last updated on 28/May/20
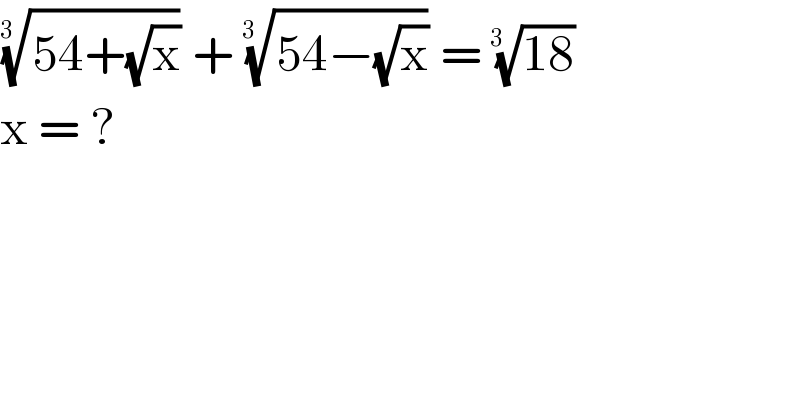
$$\sqrt[{\mathrm{3}\:\:}]{\mathrm{54}+\sqrt{\mathrm{x}}}\:+\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{54}−\sqrt{\mathrm{x}}}\:=\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{18}}\: \\ $$$$\mathrm{x}\:=\:?\: \\ $$
Answered by i jagooll last updated on 28/May/20
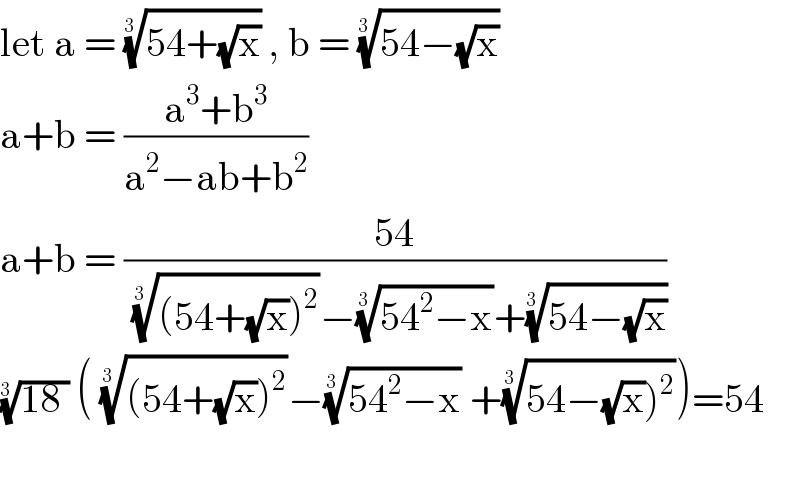
$$\mathrm{let}\:\mathrm{a}\:=\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{54}+\sqrt{\mathrm{x}}}\:,\:\mathrm{b}\:=\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{54}−\sqrt{\mathrm{x}}}\: \\ $$$$\mathrm{a}+\mathrm{b}\:=\:\frac{\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{ab}+\mathrm{b}^{\mathrm{2}} } \\ $$$$\mathrm{a}+\mathrm{b}\:=\:\frac{\mathrm{54}}{\:\sqrt[{\mathrm{3}\:\:}]{\left(\mathrm{54}+\sqrt{\mathrm{x}}\right)^{\mathrm{2}} }−\sqrt[{\mathrm{3}\:\:}]{\mathrm{54}^{\mathrm{2}} −\mathrm{x}}+\sqrt[{\mathrm{3}\:\:}]{\mathrm{54}−\sqrt{\mathrm{x}}}}\: \\ $$$$\sqrt[{\mathrm{3}\:\:}]{\mathrm{18}\:}\:\left(\:\sqrt[{\mathrm{3}\:\:}]{\left(\mathrm{54}+\sqrt{\mathrm{x}}\right)^{\mathrm{2}} }−\sqrt[{\mathrm{3}\:\:}]{\mathrm{54}^{\mathrm{2}} −\mathrm{x}}\:+\sqrt[{\mathrm{3}\:\:}]{\left.\mathrm{54}−\sqrt{\mathrm{x}}\right)^{\mathrm{2}} }\right)=\mathrm{54} \\ $$$$ \\ $$
Answered by MJS last updated on 28/May/20
![use this “trick”: a+b=c (a+b)^3 =c^3 a^3 +3a^2 b+3ab^2 +b^3 =c^3 3ab(a+b)=c^3 −a^3 −b^3 [a+b=c] 3abc=c^3 −a^3 −b^3 27a^3 b^3 c^3 =(c^3 −a^3 −b^3 )^3 in our case a=((α+β))^(1/3) ; b=((α−β))^(1/3) ; c=((18))^(1/3) 27(α+β)(α−β)18=(18−(α+β)−(α−β))^3 486(α^2 −β^2 )=(18−2α)^3 with α=54; β=(√x) 486(2916−x)=−729000 x=4416](https://www.tinkutara.com/question/Q95938.png)
$$\mathrm{use}\:\mathrm{this}\:“\mathrm{trick}'': \\ $$$${a}+{b}={c} \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} ={c}^{\mathrm{3}} \\ $$$${a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} {b}+\mathrm{3}{ab}^{\mathrm{2}} +{b}^{\mathrm{3}} ={c}^{\mathrm{3}} \\ $$$$\mathrm{3}{ab}\left({a}+{b}\right)={c}^{\mathrm{3}} −{a}^{\mathrm{3}} −{b}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\left[{a}+{b}={c}\right] \\ $$$$\mathrm{3}{abc}={c}^{\mathrm{3}} −{a}^{\mathrm{3}} −{b}^{\mathrm{3}} \\ $$$$\mathrm{27}{a}^{\mathrm{3}} {b}^{\mathrm{3}} {c}^{\mathrm{3}} =\left({c}^{\mathrm{3}} −{a}^{\mathrm{3}} −{b}^{\mathrm{3}} \right)^{\mathrm{3}} \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case}\:{a}=\sqrt[{\mathrm{3}}]{\alpha+\beta};\:{b}=\sqrt[{\mathrm{3}}]{\alpha−\beta};\:{c}=\sqrt[{\mathrm{3}}]{\mathrm{18}} \\ $$$$\mathrm{27}\left(\alpha+\beta\right)\left(\alpha−\beta\right)\mathrm{18}=\left(\mathrm{18}−\left(\alpha+\beta\right)−\left(\alpha−\beta\right)\right)^{\mathrm{3}} \\ $$$$\mathrm{486}\left(\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \right)=\left(\mathrm{18}−\mathrm{2}\alpha\right)^{\mathrm{3}} \\ $$$$\mathrm{with}\:\alpha=\mathrm{54};\:\beta=\sqrt{{x}} \\ $$$$\mathrm{486}\left(\mathrm{2916}−{x}\right)=−\mathrm{729000} \\ $$$${x}=\mathrm{4416} \\ $$
Commented by i jagooll last updated on 29/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by behi83417@gmail.com last updated on 28/May/20
![54+(√x)=a^3 ,54−(√x)=b^3 ,((18))^(1/3) =c ⇒ { ((a+b=((18))^(1/3) )),((a^3 +b^3 =108)) :} ⇒(a+b)([(a+b)^2 −3ab]=108 ⇒((18))^(1/3) .[(((18))^(1/3) )^2 −3ab]=108 ⇒18−3abc=108⇒ab=((108−18)/(−3((18))^(1/3) ))=−((30)/( ((18))^(1/3) )) ⇒a^3 .b^3 =−((27000)/(18))=−1500 { ((a^3 +b^3 =108)),((a^3 .b^3 =−1500)) :}⇒z^2 −108z−1500=0 ⇒z=[a^3 ∨b^3 ]=54±(√(54^2 +1500))=54±(√(4416)) ⇒54±(√x)=54±(√(4416))⇒x=4416 ■.](https://www.tinkutara.com/question/Q95948.png)
$$\mathrm{54}+\sqrt{\mathrm{x}}=\mathrm{a}^{\mathrm{3}} ,\mathrm{54}−\sqrt{\mathrm{x}}=\mathrm{b}^{\mathrm{3}} ,\sqrt[{\mathrm{3}}]{\mathrm{18}}=\mathrm{c} \\ $$$$\Rightarrow\begin{cases}{\mathrm{a}+\mathrm{b}=\sqrt[{\mathrm{3}}]{\mathrm{18}}}\\{\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} =\mathrm{108}}\end{cases} \\ $$$$\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)\left(\left[\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} −\mathrm{3ab}\right]=\mathrm{108}\right. \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{\mathrm{18}}.\left[\left(\sqrt[{\mathrm{3}}]{\mathrm{18}}\right)^{\mathrm{2}} −\mathrm{3ab}\right]=\mathrm{108} \\ $$$$\Rightarrow\mathrm{18}−\mathrm{3abc}=\mathrm{108}\Rightarrow\mathrm{ab}=\frac{\mathrm{108}−\mathrm{18}}{−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{18}}}=−\frac{\mathrm{30}}{\:\sqrt[{\mathrm{3}}]{\mathrm{18}}} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{3}} .\mathrm{b}^{\mathrm{3}} =−\frac{\mathrm{27000}}{\mathrm{18}}=−\mathrm{1500} \\ $$$$\begin{cases}{\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} =\mathrm{108}}\\{\mathrm{a}^{\mathrm{3}} .\mathrm{b}^{\mathrm{3}} =−\mathrm{1500}}\end{cases}\Rightarrow\mathrm{z}^{\mathrm{2}} −\mathrm{108z}−\mathrm{1500}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{z}=\left[\mathrm{a}^{\mathrm{3}} \vee\mathrm{b}^{\mathrm{3}} \right]=\mathrm{54}\pm\sqrt{\mathrm{54}^{\mathrm{2}} +\mathrm{1500}}=\mathrm{54}\pm\sqrt{\mathrm{4416}} \\ $$$$\Rightarrow\mathrm{54}\pm\sqrt{\mathrm{x}}=\mathrm{54}\pm\sqrt{\mathrm{4416}}\Rightarrow\boldsymbol{\mathrm{x}}=\mathrm{4416}\:\:\blacksquare. \\ $$
