Question Number 123780 by Ruhiyyeheyret last updated on 28/Nov/20
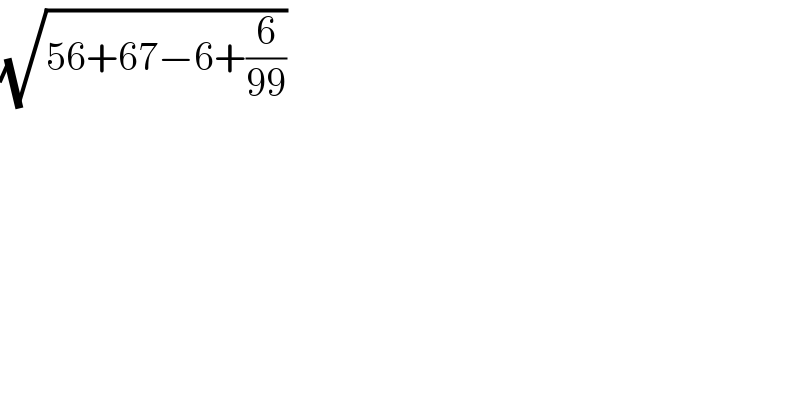
$$\sqrt{\mathrm{56}+\mathrm{67}−\mathrm{6}+\frac{\mathrm{6}}{\mathrm{99}}} \\ $$
Answered by MJS_new last updated on 28/Nov/20

$$\mathrm{1}.\:\mathrm{reduce}\:\mathrm{the}\:\mathrm{fraction}\:\frac{{a}×{c}}{{b}×{c}}=\frac{{a}}{{b}} \\ $$$$\mathrm{2}.\:\mathrm{add}/\mathrm{substract}\:\mathrm{the}\:\mathrm{integers} \\ $$$$\mathrm{3}.\:\mathrm{add}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{and}\:\mathrm{the}\:\mathrm{fraction}\:{a}+\frac{{b}}{{c}}=\frac{{ac}+{b}}{{c}} \\ $$$$\mathrm{4}.\:\mathrm{if}\:\mathrm{possible},\:\mathrm{reduce}\:\mathrm{the}\:\mathrm{fraction}\:\mathrm{again} \\ $$$$\mathrm{5}.\:\mathrm{check}\:\mathrm{both}\:\mathrm{the}\:\mathrm{numerator}\:\mathrm{and}\:\mathrm{the}\:\mathrm{denominator}\:\mathrm{for}\:\mathrm{square}\:\mathrm{factors} \\ $$$$\mathrm{6}.\:\sqrt{\frac{{a}×{b}^{\mathrm{2}} }{{c}×{d}^{\mathrm{2}} }}=\frac{{b}}{{d}}×\sqrt{\frac{{a}}{{c}}} \\ $$$$\left(\mathrm{7}.\:\mathrm{if}\:\mathrm{desired}\:\frac{{b}}{{d}}×\sqrt{\frac{{a}}{{c}}}=\frac{{b}\sqrt{{a}×{c}}}{{c}×{d}}\right) \\ $$
Commented by Ar Brandon last updated on 28/Nov/20
������ Nice one, Sir
