Menu Close

5cos-x-4sin-x-2cos-x-sin-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 54529 by tarun kunar last updated on 05/Feb/19
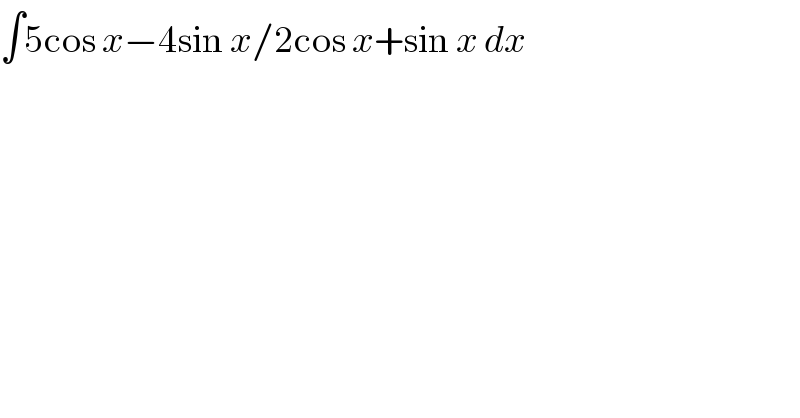
∫5cos x−4sin x/2cos x+sin x dx
$$\int\mathrm{5cos}\:{x}−\mathrm{4sin}\:{x}/\mathrm{2cos}\:{x}+\mathrm{sin}\:{x}\:{dx} \\ $$
Commented by maxmathsup by imad last updated on 05/Feb/19
let I =∫ ((5cosx−4sinx)/(2cosx +sinx))dx let use the changement tan((x/2))=t ⇒ I =∫ ((((5(1−t^2 ))/(1+t^2 ))−((8t)/(1+t^2 )))/(2((1−t^2 )/(1+t^2 )) +((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫ ((−5t^2 −8t +5)/((t^2 +1)(2−2t^2 +2t)))dt =∫ ((5t^2 +8t−5)/((t^2 +1)(t^2 −t−1)))dt let decompose F(t)=((5t^2 +8t−5)/((t^2 +1)(t^2 −t−1)))dt roots of t^2 −t−1 →Δ=1+4=5 ⇒t_1 =((1+(√5))/2) and t_2 =((1−(√5))/2) F(t)=(a/(t−t_1 )) +(b/(t−t_2 )) +((ct+d)/(t^2 +1)) a =lim_(t→t_1 ) (t−t_1 )F(t)=((5t_1 ^2 +8t_1 −5)/((t_1 ^2 +1)(√5))) b =lim_(t→t_z ) (t−t_2 )F(t)=((5t_2 ^2 +8t_2 −5)/((t_2 ^2 +1)(−(√5)))) lim_(t→+∞) tF(t)=0 =a+b +c ⇒c=−a−b F(0) =5 =−(a/t_1 ) −(b/t_2 ) +d ⇒d=5 +(a/t_1 ) +(b/t_2 ) ⇒ ∫ F(t)dt =aln∣t−t_1 ∣+bln∣t−t_2 ∣ +(c/2)ln(t^2 +1) +d arctant +λ
$${let}\:{I}\:=\int\:\frac{\mathrm{5}{cosx}−\mathrm{4}{sinx}}{\mathrm{2}{cosx}\:+{sinx}}{dx}\:\:{let}\:{use}\:{the}\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:\Rightarrow \\ $$$${I}\:=\int\:\:\frac{\frac{\mathrm{5}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{8}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{2}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\:\:\:\frac{−\mathrm{5}{t}^{\mathrm{2}} −\mathrm{8}{t}\:+\mathrm{5}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{2}{t}\right)}{dt} \\ $$$$=\int\:\:\frac{\mathrm{5}{t}^{\mathrm{2}} \:+\mathrm{8}{t}−\mathrm{5}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}−\mathrm{1}\right)}{dt}\:\:{let}\:{decompose}\:{F}\left({t}\right)=\frac{\mathrm{5}{t}^{\mathrm{2}} \:+\mathrm{8}{t}−\mathrm{5}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}−\mathrm{1}\right)}{dt} \\ $$$${roots}\:{of}\:{t}^{\mathrm{2}} −{t}−\mathrm{1}\:\rightarrow\Delta=\mathrm{1}+\mathrm{4}=\mathrm{5}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:{and}\:{t}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${F}\left({t}\right)=\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} }\:+\frac{{ct}+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow{t}_{\mathrm{1}} } \:\:\:\left({t}−{t}_{\mathrm{1}} \right){F}\left({t}\right)=\frac{\mathrm{5}{t}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{8}{t}_{\mathrm{1}} −\mathrm{5}}{\left({t}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)\sqrt{\mathrm{5}}} \\ $$$${b}\:={lim}_{{t}\rightarrow{t}_{{z}} } \left({t}−{t}_{\mathrm{2}} \right){F}\left({t}\right)=\frac{\mathrm{5}{t}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{8}{t}_{\mathrm{2}} −\mathrm{5}}{\left({t}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left(−\sqrt{\mathrm{5}}\right)} \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)=\mathrm{0}\:={a}+{b}\:+{c}\:\Rightarrow{c}=−{a}−{b} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{5}\:=−\frac{{a}}{{t}_{\mathrm{1}} }\:−\frac{{b}}{{t}_{\mathrm{2}} }\:+{d}\:\Rightarrow{d}=\mathrm{5}\:+\frac{{a}}{{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}_{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:={aln}\mid{t}−{t}_{\mathrm{1}} \mid+{bln}\mid{t}−{t}_{\mathrm{2}} \mid\:+\frac{{c}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\:+{d}\:{arctant}\:+\lambda\: \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 05/Feb/19
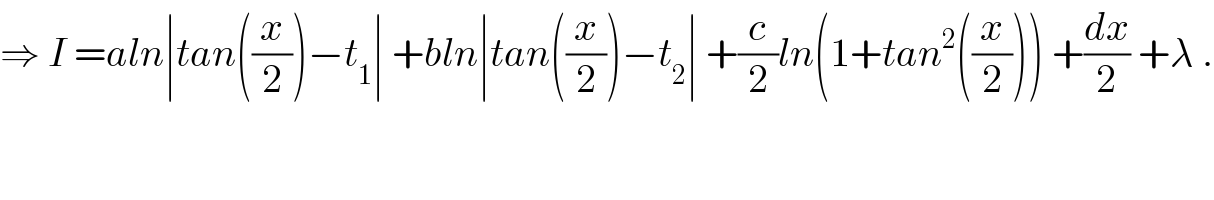
⇒ I =aln∣tan((x/2))−t_1 ∣ +bln∣tan((x/2))−t_2 ∣ +(c/2)ln(1+tan^2 ((x/2))) +(dx/2) +λ .
$$\Rightarrow\:{I}\:={aln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{t}_{\mathrm{1}} \mid\:+{bln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{t}_{\mathrm{2}} \mid\:+\frac{{c}}{\mathrm{2}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\:+\frac{{dx}}{\mathrm{2}}\:+\lambda\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Feb/19
∫((5cosx−4sinx)/(2cosx+sinx))dx ∫((a(2cosx+sinx)+b(d/dx)(2cosx+sinx))/(2cosx+sinx))dx a∫dx+b∫((d(2cosx+sinx))/(2cosx+sinx)) ax+bln(2cosx+sinx)+c now we calculate a and b 5cosx−4sinx=a(2cosx+sinx)+b(d/dx)(2cosx+sinx) 5cosx−4sinx=a(2cosx+sinx)+b(−2sinx+cosx) 5cosx−4sinx=cosx×(2a+b)+sinx×(a−2b) comparing coefficient of cosx and sinx bot side 2a+b=5 ×1 [solve it] a−2b=−4 ×2 2a+b=5 2a−4b=−8 5b=13 so b=((13)/5) 2a+b=5 2a=5−((13)/5)→ 2a=((12)/5) so a=(6/5) so answer is =(6/5)(x)+(((13)/5))ln(2cosx+sinx)+c
$$\int\frac{\mathrm{5}{cosx}−\mathrm{4}{sinx}}{\mathrm{2}{cosx}+{sinx}}{dx} \\ $$$$\int\frac{{a}\left(\mathrm{2}{cosx}+{sinx}\right)+{b}\frac{{d}}{{dx}}\left(\mathrm{2}{cosx}+{sinx}\right)}{\mathrm{2}{cosx}+{sinx}}{dx} \\ $$$${a}\int{dx}+{b}\int\frac{{d}\left(\mathrm{2}{cosx}+{sinx}\right)}{\mathrm{2}{cosx}+{sinx}} \\ $$$${ax}+{bln}\left(\mathrm{2}{cosx}+{sinx}\right)+{c} \\ $$$${now}\:{we}\:{calculate}\:{a}\:{and}\:{b} \\ $$$$\mathrm{5}{cosx}−\mathrm{4}{sinx}={a}\left(\mathrm{2}{cosx}+{sinx}\right)+{b}\frac{{d}}{{dx}}\left(\mathrm{2}{cosx}+{sinx}\right) \\ $$$$\mathrm{5}{cosx}−\mathrm{4}{sinx}={a}\left(\mathrm{2}{cosx}+{sinx}\right)+{b}\left(−\mathrm{2}{sinx}+{cosx}\right) \\ $$$$\mathrm{5}{cosx}−\mathrm{4}{sinx}={cosx}×\left(\mathrm{2}{a}+{b}\right)+{sinx}×\left({a}−\mathrm{2}{b}\right) \\ $$$${comparing}\:{coefficient}\:{of}\:{cosx}\:{and}\:{sinx}\:{bot}\:{side} \\ $$$$\mathrm{2}{a}+{b}=\mathrm{5}\:\:×\mathrm{1}\:\:\:\:\:\:\:\:\:\:\left[{solve}\:{it}\right] \\ $$$${a}−\mathrm{2}{b}=−\mathrm{4}\:×\mathrm{2} \\ $$$$\mathrm{2}{a}+{b}=\mathrm{5} \\ $$$$\mathrm{2}{a}−\mathrm{4}{b}=−\mathrm{8} \\ $$$$\mathrm{5}{b}=\mathrm{13}\:\:\:{so}\:{b}=\frac{\mathrm{13}}{\mathrm{5}} \\ $$$$\mathrm{2}{a}+{b}=\mathrm{5} \\ $$$$\mathrm{2}{a}=\mathrm{5}−\frac{\mathrm{13}}{\mathrm{5}}\rightarrow\:\:\mathrm{2}{a}=\frac{\mathrm{12}}{\mathrm{5}} \\ $$$${so}\:\:{a}=\frac{\mathrm{6}}{\mathrm{5}} \\ $$$${so}\:{answer}\:{is} \\ $$$$=\frac{\mathrm{6}}{\mathrm{5}}\left({x}\right)+\left(\frac{\mathrm{13}}{\mathrm{5}}\right){ln}\left(\mathrm{2}{cosx}+{sinx}\right)+{c} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *