Question Number 161664 by cortano last updated on 21/Dec/21
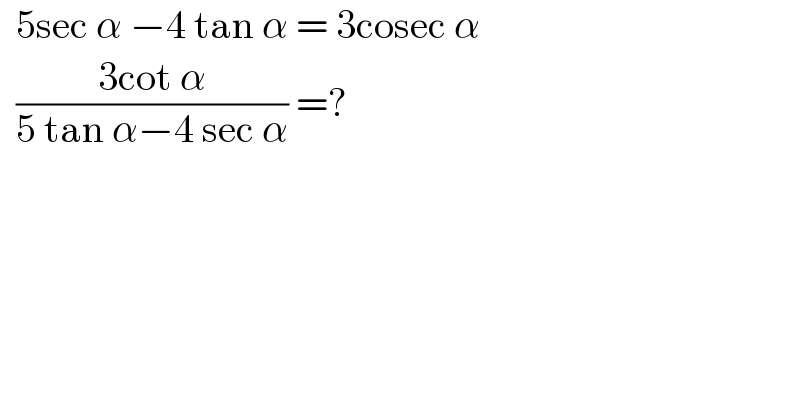
$$\:\:\mathrm{5sec}\:\alpha\:−\mathrm{4}\:\mathrm{tan}\:\alpha\:=\:\mathrm{3cosec}\:\alpha \\ $$$$\:\:\frac{\mathrm{3cot}\:\alpha}{\mathrm{5}\:\mathrm{tan}\:\alpha−\mathrm{4}\:\mathrm{sec}\:\alpha}\:=?\: \\ $$
Answered by som(math1967) last updated on 21/Dec/21
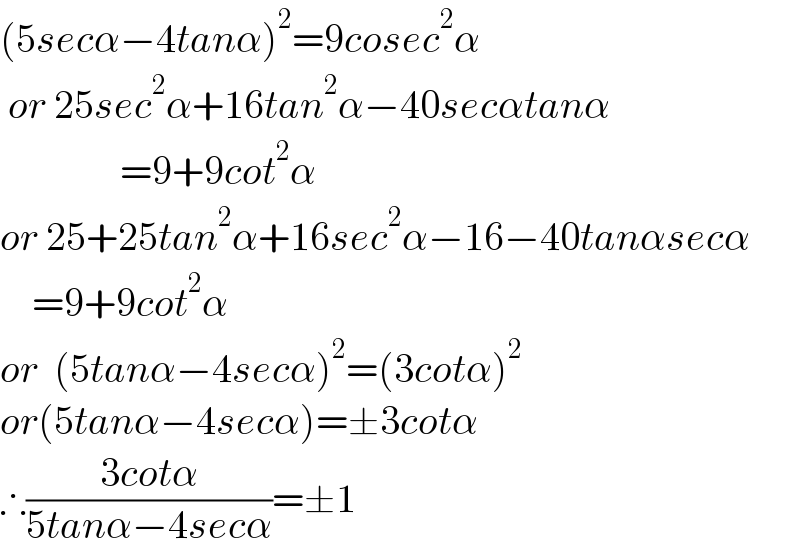
$$\left(\mathrm{5}{sec}\alpha−\mathrm{4}{tan}\alpha\right)^{\mathrm{2}} =\mathrm{9}{cosec}^{\mathrm{2}} \alpha \\ $$$$\:{or}\:\mathrm{25}{sec}^{\mathrm{2}} \alpha+\mathrm{16}{tan}^{\mathrm{2}} \alpha−\mathrm{40}{sec}\alpha{tan}\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{9}+\mathrm{9}{cot}^{\mathrm{2}} \alpha \\ $$$${or}\:\mathrm{25}+\mathrm{25}{tan}^{\mathrm{2}} \alpha+\mathrm{16}{sec}^{\mathrm{2}} \alpha−\mathrm{16}−\mathrm{40}{tan}\alpha{sec}\alpha \\ $$$$\:\:\:\:=\mathrm{9}+\mathrm{9}{cot}^{\mathrm{2}} \alpha \\ $$$${or}\:\:\left(\mathrm{5}{tan}\alpha−\mathrm{4}{sec}\alpha\right)^{\mathrm{2}} =\left(\mathrm{3}{cot}\alpha\right)^{\mathrm{2}} \\ $$$${or}\left(\mathrm{5}{tan}\alpha−\mathrm{4}{sec}\alpha\right)=\pm\mathrm{3}{cot}\alpha \\ $$$$\therefore\frac{\mathrm{3}{cot}\alpha}{\mathrm{5}{tan}\alpha−\mathrm{4}{sec}\alpha}=\pm\mathrm{1} \\ $$
