Question Number 45014 by peter frank last updated on 07/Oct/18

Commented by peter frank last updated on 07/Oct/18

Commented by peter frank last updated on 07/Oct/18
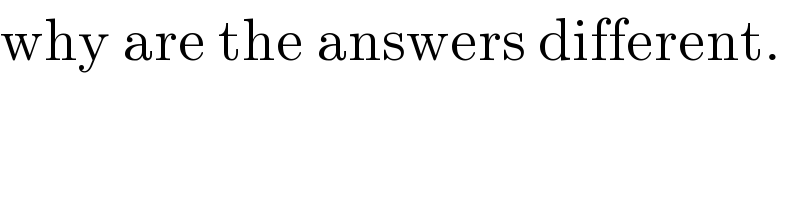
Commented by MJS last updated on 07/Oct/18
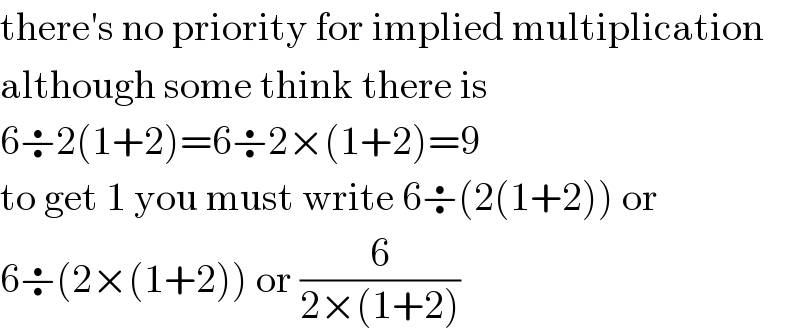
Commented by MJS last updated on 08/Oct/18
Commented by peter frank last updated on 08/Oct/18

Commented by MJS last updated on 08/Oct/18

Answered by Joel578 last updated on 07/Oct/18
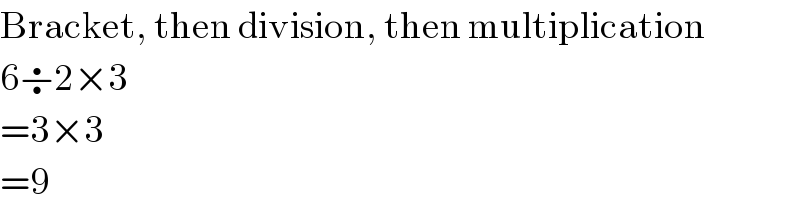
Commented by MJS last updated on 08/Oct/18

Commented by Rasheed.Sindhi last updated on 08/Oct/18

Commented by Rasheed.Sindhi last updated on 08/Oct/18

Commented by MJS last updated on 08/Oct/18

Commented by MJS last updated on 08/Oct/18

Commented by ajfour last updated on 08/Oct/18
Commented by MJS last updated on 08/Oct/18

Commented by Rasheed.Sindhi last updated on 08/Oct/18

Commented by MJS last updated on 08/Oct/18

Commented by MrW3 last updated on 08/Oct/18

Commented by Rasheed.Sindhi last updated on 09/Oct/18

Commented by Rasheed.Sindhi last updated on 09/Oct/18

Commented by Rasheed.Sindhi last updated on 09/Oct/18

