Question Number 121608 by naka3546 last updated on 10/Nov/20

$$\left(\mathrm{6}^{\mathrm{2020}} \:+\:\mathrm{8}^{\mathrm{2020}} \right)\:{mod}\:\mathrm{49}\:\:? \\ $$$${Show}\:\:{your}\:\:{elegant}\:\:{workings}\:,\:{please}. \\ $$$${Thanks}\:\:{a}\:{lot}. \\ $$
Answered by mr W last updated on 10/Nov/20
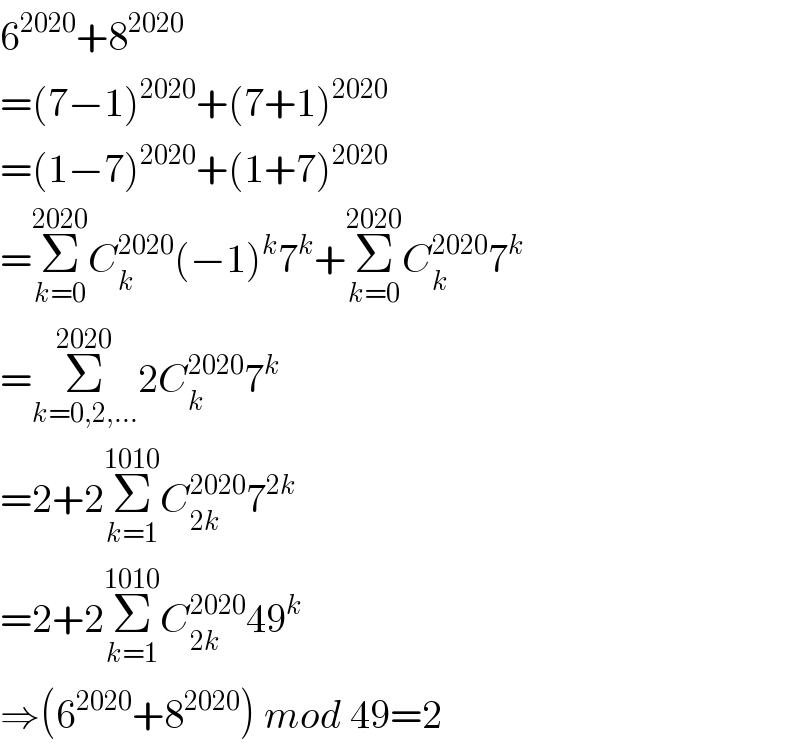
$$\mathrm{6}^{\mathrm{2020}} +\mathrm{8}^{\mathrm{2020}} \\ $$$$=\left(\mathrm{7}−\mathrm{1}\right)^{\mathrm{2020}} +\left(\mathrm{7}+\mathrm{1}\right)^{\mathrm{2020}} \\ $$$$=\left(\mathrm{1}−\mathrm{7}\right)^{\mathrm{2020}} +\left(\mathrm{1}+\mathrm{7}\right)^{\mathrm{2020}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{2020}} {\sum}}{C}_{{k}} ^{\mathrm{2020}} \left(−\mathrm{1}\right)^{{k}} \mathrm{7}^{{k}} +\underset{{k}=\mathrm{0}} {\overset{\mathrm{2020}} {\sum}}{C}_{{k}} ^{\mathrm{2020}} \mathrm{7}^{{k}} \\ $$$$=\underset{{k}=\mathrm{0},\mathrm{2},…} {\overset{\mathrm{2020}} {\sum}}\mathrm{2}{C}_{{k}} ^{\mathrm{2020}} \mathrm{7}^{{k}} \\ $$$$=\mathrm{2}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{\mathrm{1010}} {\sum}}{C}_{\mathrm{2}{k}} ^{\mathrm{2020}} \mathrm{7}^{\mathrm{2}{k}} \\ $$$$=\mathrm{2}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{\mathrm{1010}} {\sum}}{C}_{\mathrm{2}{k}} ^{\mathrm{2020}} \mathrm{49}^{{k}} \\ $$$$\Rightarrow\left(\mathrm{6}^{\mathrm{2020}} +\mathrm{8}^{\mathrm{2020}} \right)\:{mod}\:\mathrm{49}=\mathrm{2} \\ $$
Answered by Rasheed.Sindhi last updated on 10/Nov/20
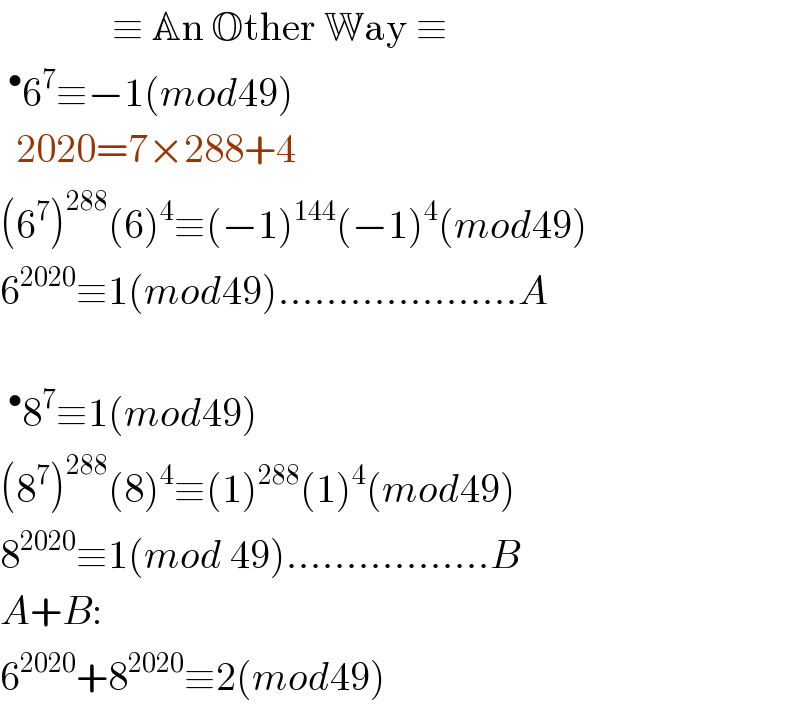
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\equiv\:\mathbb{A}\mathrm{n}\:\mathbb{O}\mathrm{ther}\:\mathbb{W}\mathrm{ay}\:\equiv \\ $$$$\:^{\bullet} \mathrm{6}^{\mathrm{7}} \equiv−\mathrm{1}\left({mod}\mathrm{49}\right)\: \\ $$$$\:\:\mathrm{2020}=\mathrm{7}×\mathrm{288}+\mathrm{4} \\ $$$$\left(\mathrm{6}^{\mathrm{7}} \right)^{\mathrm{288}} \left(\mathrm{6}\right)^{\mathrm{4}} \equiv\left(−\mathrm{1}\right)^{\mathrm{144}} \left(−\mathrm{1}\right)^{\mathrm{4}} \left({mod}\mathrm{49}\right) \\ $$$$\mathrm{6}^{\mathrm{2020}} \equiv\mathrm{1}\left({mod}\mathrm{49}\right)………………..{A} \\ $$$$ \\ $$$$\:^{\bullet} \mathrm{8}^{\mathrm{7}} \equiv\mathrm{1}\left({mod}\mathrm{49}\right) \\ $$$$\left(\mathrm{8}^{\mathrm{7}} \right)^{\mathrm{288}} \left(\mathrm{8}\right)^{\mathrm{4}} \equiv\left(\mathrm{1}\right)^{\mathrm{288}} \left(\mathrm{1}\right)^{\mathrm{4}} \left({mod}\mathrm{49}\right) \\ $$$$\mathrm{8}^{\mathrm{2020}} \equiv\mathrm{1}\left({mod}\:\mathrm{49}\right)……………..{B} \\ $$$${A}+{B}: \\ $$$$\mathrm{6}^{\mathrm{2020}} +\mathrm{8}^{\mathrm{2020}} \equiv\mathrm{2}\left({mod}\mathrm{49}\right) \\ $$
