Question Number 117475 by Dwaipayan Shikari last updated on 11/Oct/20

$$\frac{\mathrm{6}}{\mathrm{5}}.\frac{\mathrm{24}}{\mathrm{23}}.\frac{\mathrm{54}}{\mathrm{53}}.\frac{\mathrm{96}}{\mathrm{95}}.\frac{\mathrm{150}}{\mathrm{149}}.\frac{\mathrm{216}}{\mathrm{215}}.\frac{\mathrm{294}}{\mathrm{293}}…. \\ $$
Answered by frc2crc last updated on 12/Oct/20
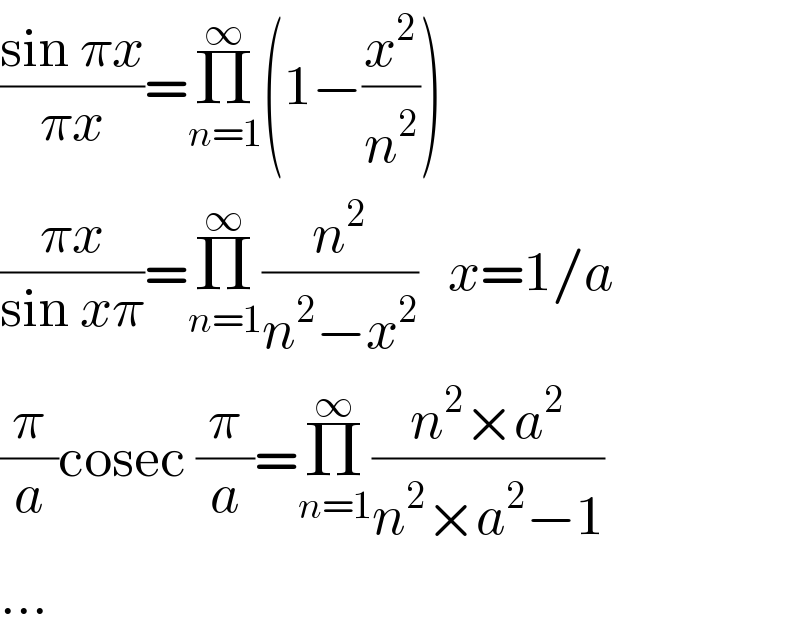
$$\frac{\mathrm{sin}\:\pi{x}}{\pi{x}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$\frac{\pi{x}}{\mathrm{sin}\:{x}\pi}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\frac{{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\:\:{x}=\mathrm{1}/{a} \\ $$$$\frac{\pi}{{a}}\mathrm{cosec}\:\frac{\pi}{{a}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\frac{{n}^{\mathrm{2}} ×{a}^{\mathrm{2}} }{{n}^{\mathrm{2}} ×{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$… \\ $$
