Question Number 164560 by PRITHWISH SEN 2 last updated on 18/Jan/22
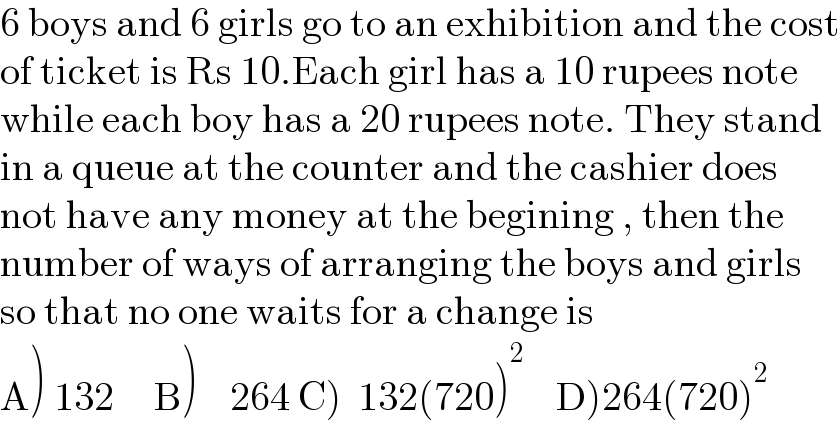
$$\mathrm{6}\:\mathrm{boys}\:\mathrm{and}\:\mathrm{6}\:\mathrm{girls}\:\mathrm{go}\:\mathrm{to}\:\mathrm{an}\:\mathrm{exhibition}\:\mathrm{and}\:\mathrm{the}\:\mathrm{cost} \\ $$$$\mathrm{of}\:\mathrm{ticket}\:\mathrm{is}\:\mathrm{Rs}\:\mathrm{10}.\mathrm{Each}\:\mathrm{girl}\:\mathrm{has}\:\mathrm{a}\:\mathrm{10}\:\mathrm{rupees}\:\mathrm{note} \\ $$$$\mathrm{while}\:\mathrm{each}\:\mathrm{boy}\:\mathrm{has}\:\mathrm{a}\:\mathrm{20}\:\mathrm{rupees}\:\mathrm{note}.\:\mathrm{They}\:\mathrm{stand}\: \\ $$$$\mathrm{in}\:\mathrm{a}\:\mathrm{queue}\:\mathrm{at}\:\mathrm{the}\:\mathrm{counter}\:\mathrm{and}\:\mathrm{the}\:\mathrm{cashier}\:\mathrm{does} \\ $$$$\mathrm{not}\:\mathrm{have}\:\mathrm{any}\:\mathrm{money}\:\mathrm{at}\:\mathrm{the}\:\mathrm{begining}\:,\:\mathrm{then}\:\mathrm{the}\: \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{of}\:\mathrm{arranging}\:\mathrm{the}\:\mathrm{boys}\:\mathrm{and}\:\mathrm{girls} \\ $$$$\mathrm{so}\:\mathrm{that}\:\mathrm{no}\:\mathrm{one}\:\mathrm{waits}\:\mathrm{for}\:\mathrm{a}\:\mathrm{change}\:\mathrm{is} \\ $$$$\left.\mathrm{A}\left.\right)\left.\:\left.\mathrm{132}\:\:\:\:\:\mathrm{B}\right)\:\:\:\:\mathrm{264}\:\mathrm{C}\right)\:\:\mathrm{132}\left(\mathrm{720}\right)^{\mathrm{2}} \:\:\:\:\mathrm{D}\right)\mathrm{264}\left(\mathrm{720}\right)^{\mathrm{2}} \\ $$
Commented by mr W last updated on 12/Mar/23

$${general}\:{solution}\:{see}\:{Q}\mathrm{189049} \\ $$
Answered by nikif99 last updated on 19/Jan/22

$$\left.{C}\right)\:\mathrm{132}\left(\mathrm{720}\right)^{\mathrm{2}} =\mathrm{68}\:\mathrm{428}\:\mathrm{800} \\ $$
Commented by PRITHWISH SEN 2 last updated on 20/Jan/22

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{But}\:\mathrm{workings}\:? \\ $$
Commented by nikif99 last updated on 20/Jan/22

$${Let}'{s}\:{ignore}\:{boys}.\:\mathrm{6}\:{girls}\:{can}\:{stand}\:{in} \\ $$$${a}\:{queue}\:{in}\:\mathrm{6}!\:{ways}.\:{Now}\:{we}\:{ignore}\:{girls}. \\ $$$$\mathrm{6}\:{boys}\:{can}\:{stand}\:{in}\:{a}\:{queue}\:{in}\:\mathrm{6}!\:{ways}. \\ $$$${Merging}\:{these}\:{queues}\:{in}\:{any}\:{way} \\ $$$${produces}\:\left(\mathrm{6}!\right)^{\mathrm{2}} =\mathrm{518400}\:{ways}\:{for} \\ $$$${reaching}\:{the}\:{cashier}.\:{Now}\:{the}\:{problem} \\ $$$${is}\:“{in}\:{how}\:{many}\:{ways}\:{can}\:{we}\:{merge} \\ $$$${these}\:{two}\:{lists}\:{with}\:{the}\:{restriction} \\ $$$$'{number}\:{of}\:{girls}\:{passed}\:>=\:{number} \\ $$$${of}\:{boys}\:{passed}'''. \\ $$$${I}\:{still}\:{look}\:{for}\:{this}\:{answer}.\:{All}\:{queues} \\ $$$${must}\:{start}\:{with}\:{girl}\:{and}\:{end}\:{with}\:{boy}. \\ $$$${Using}\:{graphic}\:{design}\:{I}\:{estimate}\:{this} \\ $$$${to}\:\mathrm{132}.\:{I}\:{suppose}\:{number}\:{of}\:{accepted} \\ $$$${mergins}\:\left(\mathrm{132}\right)\:{is}\:{combinations}\:{of}\:\mathrm{12} \\ $$$${over}\:\mathrm{6}\:\left({C}_{\mathrm{6}} ^{\mathrm{12}} \right)\:{minus}\:\mathrm{792}\:{which}\:{represent} \\ $$$${queues}\:{not}\:{fullfilling}\:{the}\:{restriction} \\ $$$$\left({need}\:{to}\:{explore}\:{how}\:{to}\:{compute}\:{it}\right). \\ $$$${If}\:{someone}\:{else}\:{could}\:{advance}\:{to}\:{a} \\ $$$${solution}\:{I}\:{would}\:{be}\:{happy}\:{to}\:{read}. \\ $$
Answered by mr W last updated on 24/Jan/22

$$\blacktriangleleft\:{GB}_{\mathrm{1}} {GB}_{\mathrm{2}} {GB}_{\mathrm{3}} {GB}_{\mathrm{4}} {GB}_{\mathrm{5}} {GB}_{\mathrm{6}} \\ $$$${G}={positions}\:{of}\:{the}\:{girls} \\ $$$${B}_{{i}} ={possible}\:{positions}\:{of}\:{boys} \\ $$$${a}={number}\:{of}\:{boys}\:{at}\:{position}\:{B}_{\mathrm{1}} \\ $$$${b}={number}\:{of}\:{boys}\:{at}\:{position}\:{B}_{\mathrm{2}} \\ $$$$… \\ $$$${f}={number}\:{of}\:{boys}\:{at}\:{position}\:{B}_{\mathrm{6}} \\ $$$${a}+{b}+{c}+{d}+{e}+{f}=\mathrm{6} \\ $$$$\mathrm{0}\leqslant{a}\leqslant\mathrm{1} \\ $$$$\mathrm{0}\leqslant{b}\leqslant\mathrm{2}−{a} \\ $$$$\mathrm{0}\leqslant{c}\leqslant\mathrm{3}−{a}−{b} \\ $$$$\mathrm{0}\leqslant{d}\leqslant\mathrm{4}−{a}−{b}−{c} \\ $$$$\mathrm{0}\leqslant{e}\leqslant\mathrm{5}−{a}−{b}−{c}−{d} \\ $$$$\mathrm{0}\leqslant{f}\leqslant\mathrm{6}−{a}−{b}−{c}−{d}−{e} \\ $$$${number}\:{of}\:{ways}\:{to}\:{place}\:{the}\:\mathrm{6}\:{boys} \\ $$$${into}\:{the}\:{proper}\:{positions}\:{is} \\ $$$${n}=\underset{{a}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}\:\underset{{b}=\mathrm{0}} {\overset{\mathrm{2}−{a}} {\sum}}\:\underset{{c}=\mathrm{0}} {\overset{\mathrm{3}−{a}−{b}} {\sum}}\:\underset{{d}=\mathrm{0}} {\overset{\mathrm{4}−{a}−{b}−{c}} {\sum}}\:\underset{{e}=\mathrm{0}} {\overset{\mathrm{5}−{a}−{b}−{c}−{d}} {\sum}}\:\underset{{f}=\mathrm{0}} {\overset{\mathrm{6}−{a}−{b}−{c}−{d}−{e}} {\sum}}{if}\:\left({a}+{b}+{c}+{d}+{e}+{f}=\mathrm{6}\right) \\ $$$${we}\:{get}\:{n}=\mathrm{132}. \\ $$$${in}\:{each}\:{of}\:{these}\:{arrangements}\:{we} \\ $$$${have}\:\mathrm{6}!=\mathrm{720}\:{ways}\:{to}\:{arrange}\:{the}\:{boys} \\ $$$${and}\:\mathrm{6}!=\mathrm{720}\:{ways}\:{to}\:{arrange}\:{the}\:{girls}. \\ $$$${so}\:{the}\:{total}\:{number}\:{of}\:{ways}\:{to} \\ $$$${queue}\:{the}\:{boys}\:{and}\:{girls}\:{properly}\:{is}\: \\ $$$$\mathrm{132}×\left(\mathrm{720}\right)^{\mathrm{2}} . \\ $$
Commented by mr W last updated on 25/Jan/22
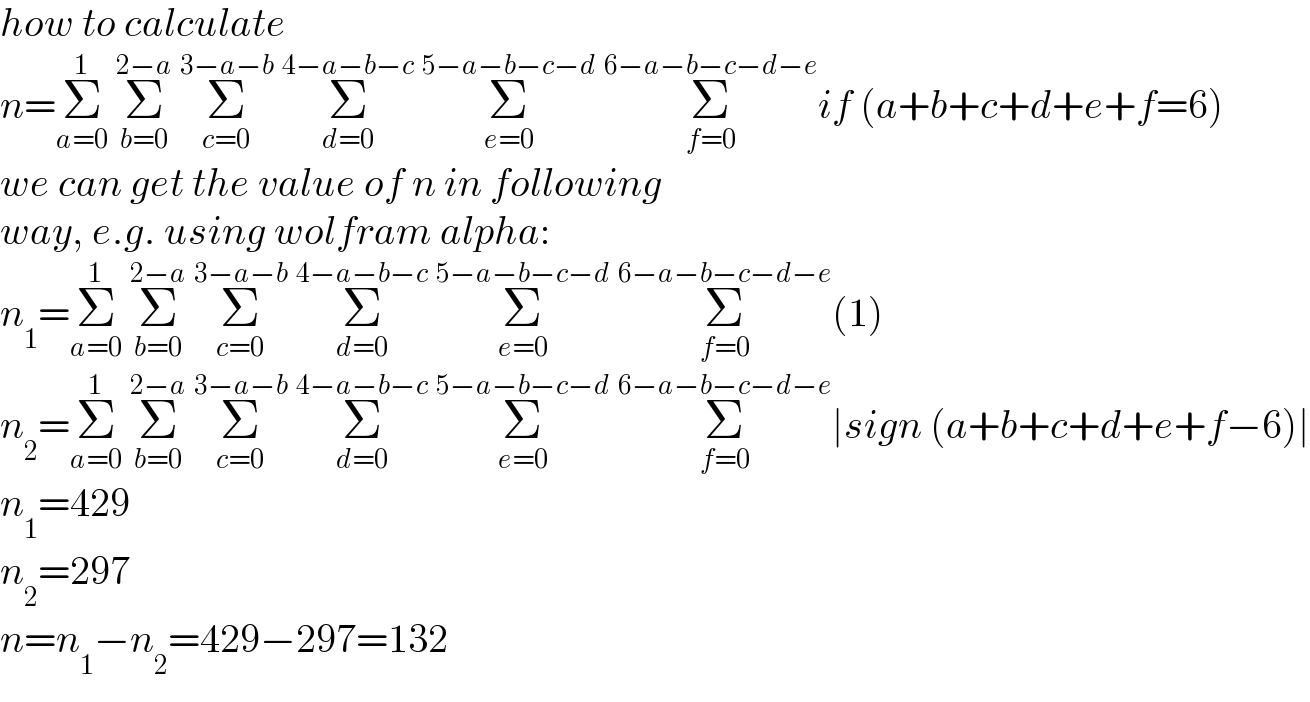
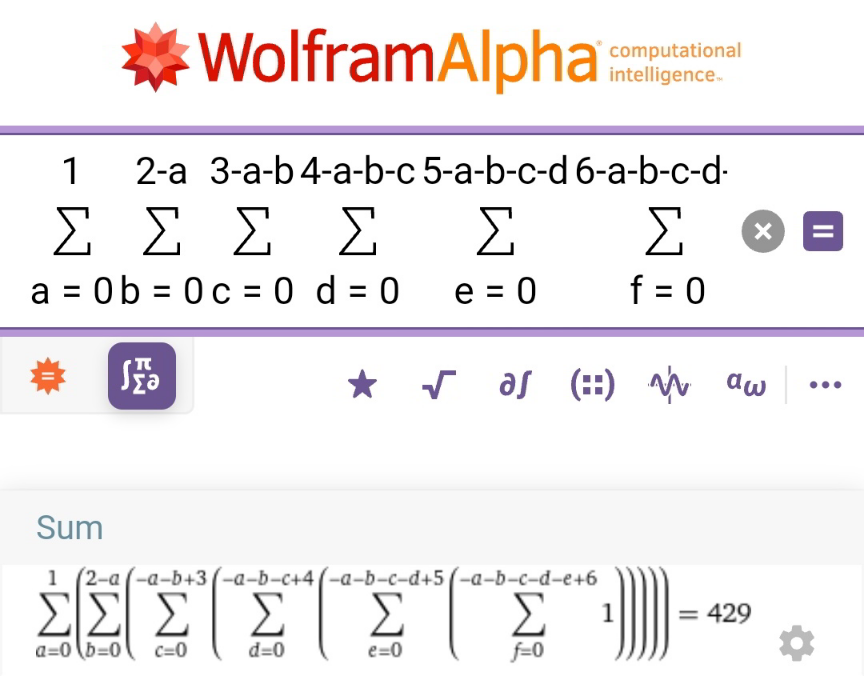
$${how}\:{to}\:{calculate} \\ $$$${n}=\underset{{a}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}\:\underset{{b}=\mathrm{0}} {\overset{\mathrm{2}−{a}} {\sum}}\:\underset{{c}=\mathrm{0}} {\overset{\mathrm{3}−{a}−{b}} {\sum}}\:\underset{{d}=\mathrm{0}} {\overset{\mathrm{4}−{a}−{b}−{c}} {\sum}}\:\underset{{e}=\mathrm{0}} {\overset{\mathrm{5}−{a}−{b}−{c}−{d}} {\sum}}\:\underset{{f}=\mathrm{0}} {\overset{\mathrm{6}−{a}−{b}−{c}−{d}−{e}} {\sum}}{if}\:\left({a}+{b}+{c}+{d}+{e}+{f}=\mathrm{6}\right) \\ $$$${we}\:{can}\:{get}\:{the}\:{value}\:{of}\:{n}\:{in}\:{following} \\ $$$${way},\:{e}.{g}.\:{using}\:{wolfram}\:{alpha}: \\ $$$${n}_{\mathrm{1}} =\underset{{a}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}\:\underset{{b}=\mathrm{0}} {\overset{\mathrm{2}−{a}} {\sum}}\:\underset{{c}=\mathrm{0}} {\overset{\mathrm{3}−{a}−{b}} {\sum}}\:\underset{{d}=\mathrm{0}} {\overset{\mathrm{4}−{a}−{b}−{c}} {\sum}}\:\underset{{e}=\mathrm{0}} {\overset{\mathrm{5}−{a}−{b}−{c}−{d}} {\sum}}\:\underset{{f}=\mathrm{0}} {\overset{\mathrm{6}−{a}−{b}−{c}−{d}−{e}} {\sum}}\left(\mathrm{1}\right) \\ $$$${n}_{\mathrm{2}} =\underset{{a}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}\:\underset{{b}=\mathrm{0}} {\overset{\mathrm{2}−{a}} {\sum}}\:\underset{{c}=\mathrm{0}} {\overset{\mathrm{3}−{a}−{b}} {\sum}}\:\underset{{d}=\mathrm{0}} {\overset{\mathrm{4}−{a}−{b}−{c}} {\sum}}\:\underset{{e}=\mathrm{0}} {\overset{\mathrm{5}−{a}−{b}−{c}−{d}} {\sum}}\:\underset{{f}=\mathrm{0}} {\overset{\mathrm{6}−{a}−{b}−{c}−{d}−{e}} {\sum}}\mid{sign}\:\left({a}+{b}+{c}+{d}+{e}+{f}−\mathrm{6}\right)\mid \\ $$$${n}_{\mathrm{1}} =\mathrm{429} \\ $$$${n}_{\mathrm{2}} =\mathrm{297} \\ $$$${n}={n}_{\mathrm{1}} −{n}_{\mathrm{2}} =\mathrm{429}−\mathrm{297}=\mathrm{132} \\ $$
Commented by mr W last updated on 25/Jan/22
Commented by mr W last updated on 25/Jan/22
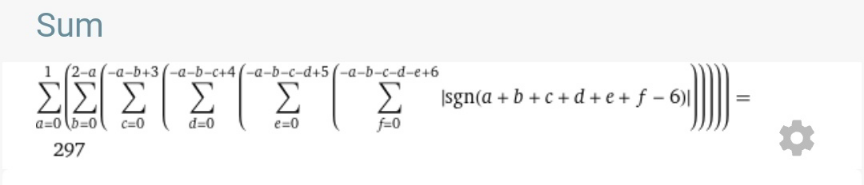
Commented by nikif99 last updated on 30/Jan/22
$${A}\:{wonderfull}\:{solution}\:{to}\:{a}\:{complicated} \\ $$$${problem}.\:{Thank}\:{you}\:{Sir}\:{W}\:{for}\:{your} \\ $$$${contribution}. \\ $$
Commented by Ar Brandon last updated on 30/Jan/22
Q161675 , Sir ��
