Question Number 159008 by amin96 last updated on 11/Nov/21
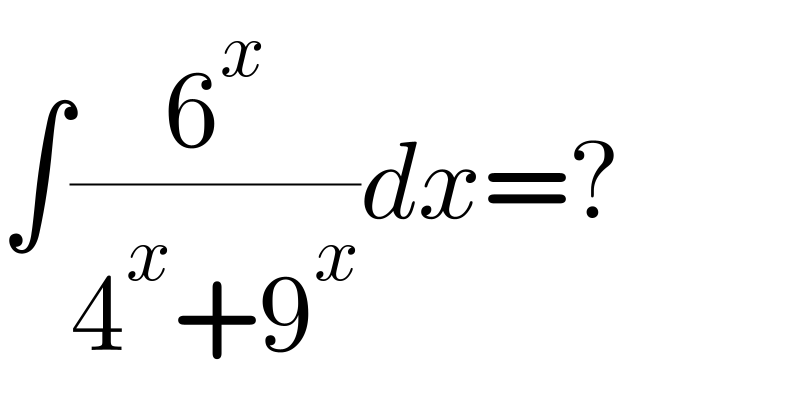
$$\int\frac{\mathrm{6}^{{x}} }{\mathrm{4}^{{x}} +\mathrm{9}^{{x}} }{dx}=? \\ $$
Answered by qaz last updated on 11/Nov/21
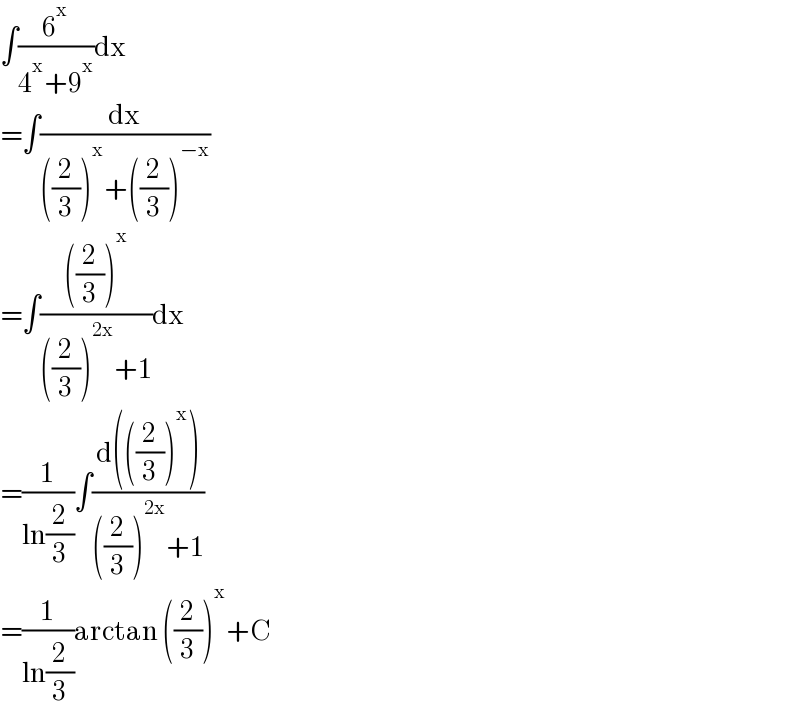
$$\int\frac{\mathrm{6}^{\mathrm{x}} }{\mathrm{4}^{\mathrm{x}} +\mathrm{9}^{\mathrm{x}} }\mathrm{dx} \\ $$$$=\int\frac{\mathrm{dx}}{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} +\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{−\mathrm{x}} } \\ $$$$=\int\frac{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} }{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2x}} +\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{ln}\frac{\mathrm{2}}{\mathrm{3}}}\int\frac{\mathrm{d}\left(\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \right)}{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2x}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{ln}\frac{\mathrm{2}}{\mathrm{3}}}\mathrm{arctan}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} +\mathrm{C} \\ $$
