Menu Close

6-x-x-5-x-help-me-

Tinku Tara 0 Comments
Pin




Question Number 99621 by student work last updated on 22/Jun/20
6^x =x^(5 ) x=? help me
$$\mathrm{6}^{\mathrm{x}} =\mathrm{x}^{\mathrm{5}\:\:\:\:\:\:\:} \mathrm{x}=?\:\:\:\:\:\:\:\mathrm{help}\:\mathrm{me} \\ $$
Commented by Dwaipayan Shikari last updated on 22/Jun/20
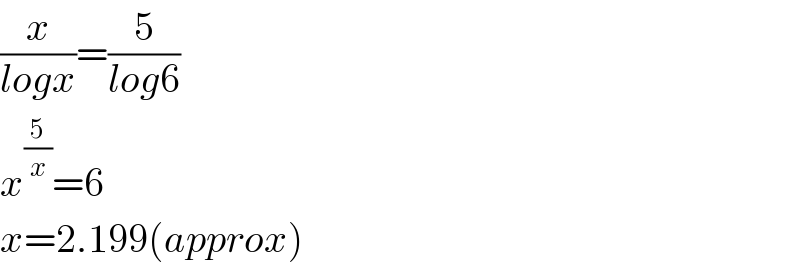
(x/(logx))=(5/(log6)) x^(5/x) =6 x=2.199(approx)
$$\frac{{x}}{{logx}}=\frac{\mathrm{5}}{{log}\mathrm{6}} \\ $$$${x}^{\frac{\mathrm{5}}{{x}}} =\mathrm{6} \\ $$$${x}=\mathrm{2}.\mathrm{199}\left({approx}\right) \\ $$
Answered by MWSuSon last updated on 22/Jun/20
ln6^x =lnx^5 ⇔xln6=5lnx ⇔(1/5)ln6=x^(−1) lnx ⇔(1/5)ln6=e^(lnx^(−1) ) lnx ⇔−(1/5)ln6=−lnxe^(−lnx) W_0 (−(1/5)ln6)=W_0 (−lnxe^(−lnx) ) since −(1/5)ln6>−(1/e) we use both p− rincipal and −1 branch. −lnx=W_p (−(1/5)ln6) lnx=−W_p (−(1/5)ln6) x=e^(−W_p (−(1/5)ln6)) x=2.1991 Looking at the −1 branch x=^(−W_(−1) (−(1/5)ln6)) x=3.4795 ⇒for 6^x =x^5 x= { ((2.1991, W_p )),((3.4795, W_(−1) )) :} W_0 is the lambert W function also called product log.
$$\mathrm{ln6}^{\mathrm{x}} =\mathrm{lnx}^{\mathrm{5}} \\ $$$$\Leftrightarrow\mathrm{xln6}=\mathrm{5lnx} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln6}=\mathrm{x}^{−\mathrm{1}} \mathrm{lnx} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln6}=\mathrm{e}^{\mathrm{lnx}^{−\mathrm{1}} } \mathrm{lnx} \\ $$$$\Leftrightarrow−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln6}=−\mathrm{lnxe}^{−\mathrm{lnx}} \\ $$$$\mathrm{W}_{\mathrm{0}} \left(−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln6}\right)=\mathrm{W}_{\mathrm{0}} \left(−\mathrm{lnxe}^{−\mathrm{lnx}} \right) \\ $$$$\mathrm{since}\:−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln6}>−\frac{\mathrm{1}}{\mathrm{e}}\:\mathrm{we}\:\mathrm{use}\:\mathrm{both}\:\mathrm{p}− \\ $$$$\mathrm{rincipal}\:\mathrm{and}\:−\mathrm{1}\:\mathrm{branch}. \\ $$$$−\mathrm{lnx}=\mathrm{W}_{\mathrm{p}} \left(−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln6}\right) \\ $$$$\mathrm{lnx}=−\mathrm{W}_{\mathrm{p}} \left(−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln6}\right) \\ $$$$\mathrm{x}=\mathrm{e}^{−\mathrm{W}_{\mathrm{p}} \left(−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln6}\right)} \\ $$$$\mathrm{x}=\mathrm{2}.\mathrm{1991} \\ $$$$\mathrm{Looking}\:\mathrm{at}\:\mathrm{the}\:−\mathrm{1}\:\mathrm{branch} \\ $$$$\mathrm{x}=^{−\mathrm{W}_{−\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln6}\right)} \\ $$$$\mathrm{x}=\mathrm{3}.\mathrm{4795} \\ $$$$\Rightarrow\mathrm{for}\:\mathrm{6}^{\mathrm{x}} =\mathrm{x}^{\mathrm{5}} \\ $$$$\mathrm{x}=\begin{cases}{\mathrm{2}.\mathrm{1991},\:\:\:\:\mathrm{W}_{\mathrm{p}} }\\{\mathrm{3}.\mathrm{4795},\:\:\:\:\mathrm{W}_{−\mathrm{1}} }\end{cases} \\ $$$$\mathrm{W}_{\mathrm{0}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{lambert}\:\mathrm{W}\:\mathrm{function}\:\mathrm{also} \\ $$$$\mathrm{called}\:\mathrm{product}\:\mathrm{log}. \\ $$
Answered by mr W last updated on 22/Jun/20
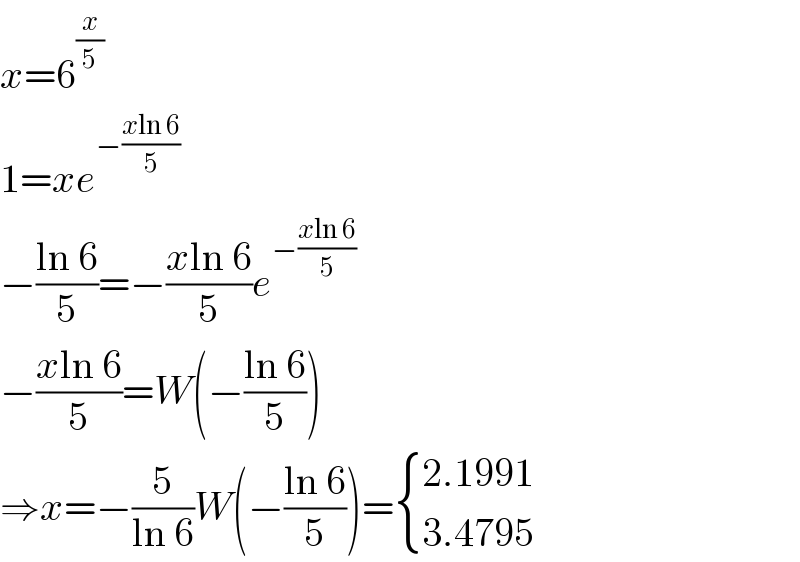
x=6^(x/5) 1=xe^(−((xln 6)/5)) −((ln 6)/5)=−((xln 6)/5)e^(−((xln 6)/5)) −((xln 6)/5)=W(−((ln 6)/5)) ⇒x=−(5/(ln 6))W(−((ln 6)/5))= { ((2.1991)),((3.4795)) :}
$${x}=\mathrm{6}^{\frac{{x}}{\mathrm{5}}} \\ $$$$\mathrm{1}={xe}^{−\frac{{x}\mathrm{ln}\:\mathrm{6}}{\mathrm{5}}} \\ $$$$−\frac{\mathrm{ln}\:\mathrm{6}}{\mathrm{5}}=−\frac{{x}\mathrm{ln}\:\mathrm{6}}{\mathrm{5}}{e}^{−\frac{{x}\mathrm{ln}\:\mathrm{6}}{\mathrm{5}}} \\ $$$$−\frac{{x}\mathrm{ln}\:\mathrm{6}}{\mathrm{5}}={W}\left(−\frac{\mathrm{ln}\:\mathrm{6}}{\mathrm{5}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathrm{5}}{\mathrm{ln}\:\mathrm{6}}{W}\left(−\frac{\mathrm{ln}\:\mathrm{6}}{\mathrm{5}}\right)=\begin{cases}{\mathrm{2}.\mathrm{1991}}\\{\mathrm{3}.\mathrm{4795}}\end{cases} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *