Menu Close

60-abc-nm000-0-m-n-

Tinku Tara 0 Comments
Pin




Question Number 164628 by amin96 last updated on 19/Jan/22
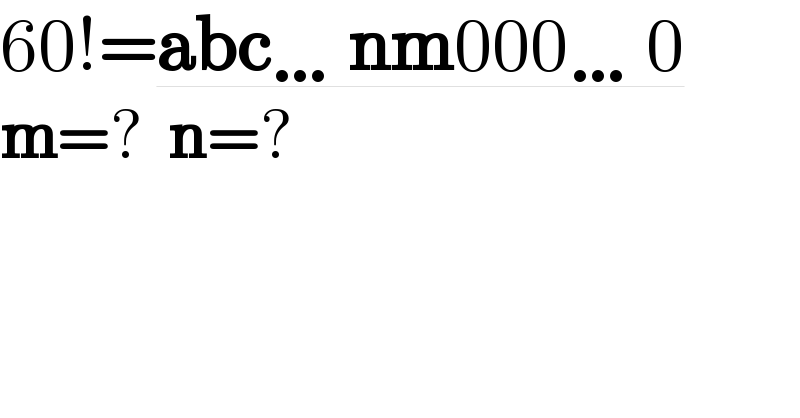
60!=abc…nm000…0 m=? n=?
$$\mathrm{60}!=\underline{\boldsymbol{\mathrm{abc}}\ldots\boldsymbol{\mathrm{nm}}\mathrm{000}\ldots\mathrm{0}} \\ $$$$\boldsymbol{\mathrm{m}}=?\:\:\boldsymbol{\mathrm{n}}=? \\ $$
Commented by amin96 last updated on 20/Jan/22
answer 9; 6
$$\boldsymbol{\mathrm{answer}}\:\mathrm{9};\:\mathrm{6} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 20/Jan/22
60!=abc…nm000…0 60!=abc…nm000…0 ;^(−) m=? n=? ^• Counting of factor 5: ⌊((60)/5)⌋+⌊((60)/5^2 )⌋=12+2=14 ^• Counting of factor 2: ⌊((60)/2)⌋+⌊((60)/2^2 )⌋+⌊((60)/2^3 )⌋+⌊((60)/2^4 )⌋+⌊((60)/2^5 )⌋ =30+15+7+3+1=56 ^• ((60!)/(2^(14) ∙5^(14) ))=abc…nm ^(−) Similar process can help us to determine number of each prime factor under sixty in ((60!)/(2^(14) ∙5^(14) ))=abc…nm ^(−) .There′s no factor 5 of course and number of 2′s is now 56−14=42 Hence ((60!)/(2^(14) ∙5^(14) ))=abc…nm ^(−) now can be factorized as: 2^(42) .3^(28) .7^9 .11^5 .13^4 .17^3 .19^3 .23^2 .29^2 .31.37.41.43.47.53.59 Now, ((60!)/(2^(14) ∙5^(14) ))=abc…nm ^(−) ≡^(100) nm^(−) ^• 2^(22) ≡^(100) 4⇒(2^(22) )^2 ≡^(100) 4^2 =16⇒2^(44) ≡^(100) 16 ⇒2^(44) /2^2 ≡^(100) 16/4=4⇒ 2^(42) ≡^(100) 4 ^• 3^(20) ≡^(100) 1∧3^8 ≡^(100) 61⇒3^(28) ≡^(100) 61 ^• 7^4 ≡^(100) 1⇒(7^4 )^2 .7≡7⇒7^9 ≡^(100) 7 ^• 11^5 ≡^(100) 51 ^• 13^4 ≡^(100) 61 ^• 17^3 ≡^(100) 13 ^• 19^3 ≡^(100) 59 ^• 23^2 ≡^(100) 29 ^• 29^2 ≡^(100) 41 ^• 31 ≡^(100) 31 ^• 37 ≡^(100) 37 ^• 41 ≡^(100) 41 ^• 43 ≡^(100) 43 ^• 47 ≡^(100) 47 ^• 53 ≡^(100) 53 ^• 59 ≡^(100) 59 Multiplying blue congruences (for convenience use modular multiplication) abc…nm ^(−) ≡^(100) 96
$$\mathrm{60}!=\underline{\boldsymbol{\mathrm{abc}}\ldots\boldsymbol{\mathrm{nm}}\mathrm{000}\ldots\mathrm{0}} \\ $$$$\mathrm{60}!\overline {={abc}\ldots{nm}\mathrm{000}\ldots\mathrm{0}\:\:;}\:{m}=?\:\:{n}=? \\ $$$$\:^{\bullet} \mathrm{Counting}\:\mathrm{of}\:\mathrm{factor}\:\mathrm{5}: \\ $$$$\:\:\lfloor\frac{\mathrm{60}}{\mathrm{5}}\rfloor+\lfloor\frac{\mathrm{60}}{\mathrm{5}^{\mathrm{2}} }\rfloor=\mathrm{12}+\mathrm{2}=\mathrm{14} \\ $$$$\:^{\bullet} \mathrm{Counting}\:\mathrm{of}\:\mathrm{factor}\:\mathrm{2}: \\ $$$$\:\:\lfloor\frac{\mathrm{60}}{\mathrm{2}}\rfloor+\lfloor\frac{\mathrm{60}}{\mathrm{2}^{\mathrm{2}} }\rfloor+\lfloor\frac{\mathrm{60}}{\mathrm{2}^{\mathrm{3}} }\rfloor+\lfloor\frac{\mathrm{60}}{\mathrm{2}^{\mathrm{4}} }\rfloor+\lfloor\frac{\mathrm{60}}{\mathrm{2}^{\mathrm{5}} }\rfloor \\ $$$$=\mathrm{30}+\mathrm{15}+\mathrm{7}+\mathrm{3}+\mathrm{1}=\mathrm{56} \\ $$$$\:^{\bullet} \frac{\mathrm{60}!}{\mathrm{2}^{\mathrm{14}} \centerdot\mathrm{5}^{\mathrm{14}} }\overline {={abc}\ldots{nm}\:\:\:} \\ $$$$\mathrm{Similar}\:\mathrm{process}\:\mathrm{can}\:\mathrm{help}\:\mathrm{us}\:\mathrm{to}\:\mathrm{determine} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{each}\:\mathrm{prime}\:\mathrm{factor}\:\mathrm{under} \\ $$$$\mathrm{sixty}\:\mathrm{in}\:\:\frac{\mathrm{60}!}{\mathrm{2}^{\mathrm{14}} \centerdot\mathrm{5}^{\mathrm{14}} }\overline {={abc}\ldots{nm}\:\:\:}.\mathrm{There}'\mathrm{s} \\ $$$$\mathrm{no}\:\mathrm{factor}\:\mathrm{5}\:\mathrm{of}\:\mathrm{course}\:\mathrm{and}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{2}'\mathrm{s}\:\mathrm{is}\:\mathrm{now}\:\mathrm{56}−\mathrm{14}=\mathrm{42} \\ $$$$\mathrm{Hence}\:\:\:\frac{\mathrm{60}!}{\mathrm{2}^{\mathrm{14}} \centerdot\mathrm{5}^{\mathrm{14}} }\overline {={abc}\ldots{nm}\:\:\:}\mathrm{now}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{factorized}\:\mathrm{as}: \\ $$$$\mathrm{2}^{\mathrm{42}} .\mathrm{3}^{\mathrm{28}} .\mathrm{7}^{\mathrm{9}} .\mathrm{11}^{\mathrm{5}} .\mathrm{13}^{\mathrm{4}} .\mathrm{17}^{\mathrm{3}} .\mathrm{19}^{\mathrm{3}} .\mathrm{23}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.\mathrm{29}^{\mathrm{2}} .\mathrm{31}.\mathrm{37}.\mathrm{41}.\mathrm{43}.\mathrm{47}.\mathrm{53}.\mathrm{59} \\ $$$${Now},\: \\ $$$$\:\frac{\mathrm{60}!}{\mathrm{2}^{\mathrm{14}} \centerdot\mathrm{5}^{\mathrm{14}} }\overline {={abc}\ldots{nm}\:}\overset{\mathrm{100}} {\equiv}\:\:\overline {{nm}} \\ $$$$\:^{\bullet} \mathrm{2}^{\mathrm{22}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{4}\Rightarrow\left(\mathrm{2}^{\mathrm{22}} \right)^{\mathrm{2}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{4}^{\mathrm{2}} =\mathrm{16}\Rightarrow\mathrm{2}^{\mathrm{44}} \:\:\overset{\mathrm{100}} {\equiv}\:\mathrm{16}\:\: \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{44}} /\mathrm{2}^{\mathrm{2}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{16}/\mathrm{4}=\mathrm{4}\Rightarrow\:\mathrm{2}^{\mathrm{42}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{4} \\ $$$$\:^{\bullet} \mathrm{3}^{\mathrm{20}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{1}\wedge\mathrm{3}^{\mathrm{8}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{61}\Rightarrow\mathrm{3}^{\mathrm{28}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{61} \\ $$$$\:^{\bullet} \mathrm{7}^{\mathrm{4}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{1}\Rightarrow\left(\mathrm{7}^{\mathrm{4}} \right)^{\mathrm{2}} .\mathrm{7}\equiv\mathrm{7}\Rightarrow\mathrm{7}^{\mathrm{9}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{7} \\ $$$$\:^{\bullet} \mathrm{11}^{\mathrm{5}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{51} \\ $$$$\:^{\bullet} \mathrm{13}^{\mathrm{4}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{61} \\ $$$$\:^{\bullet} \mathrm{17}^{\mathrm{3}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{13} \\ $$$$\:^{\bullet} \mathrm{19}^{\mathrm{3}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{59} \\ $$$$\:^{\bullet} \mathrm{23}^{\mathrm{2}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{29} \\ $$$$\:^{\bullet} \mathrm{29}^{\mathrm{2}} \:\overset{\mathrm{100}} {\equiv}\:\mathrm{41} \\ $$$$\:^{\bullet} \mathrm{31}\:\overset{\mathrm{100}} {\equiv}\:\mathrm{31} \\ $$$$\:^{\bullet} \mathrm{37}\:\overset{\mathrm{100}} {\equiv}\:\mathrm{37} \\ $$$$\:^{\bullet} \mathrm{41}\:\overset{\mathrm{100}} {\equiv}\:\mathrm{41} \\ $$$$\:^{\bullet} \mathrm{43}\:\overset{\mathrm{100}} {\equiv}\:\mathrm{43} \\ $$$$\:^{\bullet} \mathrm{47}\:\overset{\mathrm{100}} {\equiv}\:\mathrm{47} \\ $$$$\:^{\bullet} \mathrm{53}\:\overset{\mathrm{100}} {\equiv}\:\mathrm{53} \\ $$$$\:^{\bullet} \mathrm{59}\:\overset{\mathrm{100}} {\equiv}\:\mathrm{59} \\ $$$$\mathrm{Multiplying}\:\mathrm{blue}\:\mathrm{congruences}\:\left(\mathrm{for}\right. \\ $$$$\left.\mathrm{convenience}\:\mathrm{use}\:\mathrm{modular}\:\mathrm{multiplication}\right) \\ $$$$\overline {\:\:\:{abc}\ldots{nm}\:\:\:}\overset{\mathrm{100}} {\equiv}\:\mathrm{96} \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jan/22
abc…nm ^(−) ≡^(100) 4.61.7.51.61.13.59.29.41.31.37.41.43.47.53.59 abc…nm ^(−) ≡^(100) (4.61).(7.51).(61.13).(59.29).(41.31).(37.41).(43.47).(53.59) ≡^(100) 44.57.93.11.71.17.21.27 ≡^(100) (44.57).(93.11).(71.17).(21.27) ≡^(100) 08.23.07.67 ≡^(100) (08.23).(07.67) ≡^(100) 84.69 ≡^(100) 96
$$\overline {\:\:\:{abc}\ldots{nm}\:\:}\:\overset{\mathrm{100}} {\equiv}\mathrm{4}.\mathrm{61}.\mathrm{7}.\mathrm{51}.\mathrm{61}.\mathrm{13}.\mathrm{59}.\mathrm{29}.\mathrm{41}.\mathrm{31}.\mathrm{37}.\mathrm{41}.\mathrm{43}.\mathrm{47}.\mathrm{53}.\mathrm{59} \\ $$$$\overline {\:\:\:{abc}\ldots{nm}\:\:}\:\overset{\mathrm{100}} {\equiv}\left(\mathrm{4}.\mathrm{61}\right).\left(\mathrm{7}.\mathrm{51}\right).\left(\mathrm{61}.\mathrm{13}\right).\left(\mathrm{59}.\mathrm{29}\right).\left(\mathrm{41}.\mathrm{31}\right).\left(\mathrm{37}.\mathrm{41}\right).\left(\mathrm{43}.\mathrm{47}\right).\left(\mathrm{53}.\mathrm{59}\right) \\ $$$$\overset{\mathrm{100}} {\equiv}\mathrm{44}.\mathrm{57}.\mathrm{93}.\mathrm{11}.\mathrm{71}.\mathrm{17}.\mathrm{21}.\mathrm{27} \\ $$$$\overset{\mathrm{100}} {\equiv}\left(\mathrm{44}.\mathrm{57}\right).\left(\mathrm{93}.\mathrm{11}\right).\left(\mathrm{71}.\mathrm{17}\right).\left(\mathrm{21}.\mathrm{27}\right) \\ $$$$\overset{\mathrm{100}} {\equiv}\mathrm{08}.\mathrm{23}.\mathrm{07}.\mathrm{67} \\ $$$$\overset{\mathrm{100}} {\equiv}\left(\mathrm{08}.\mathrm{23}\right).\left(\mathrm{07}.\mathrm{67}\right) \\ $$$$\overset{\mathrm{100}} {\equiv}\mathrm{84}.\mathrm{69} \\ $$$$\overset{\mathrm{100}} {\equiv}\mathrm{96} \\ $$
Commented by mr W last updated on 21/Jan/22
very nice solution!
$${very}\:{nice}\:{solution}! \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jan/22
Grateful sir mr W!
$$\mathcal{G}{rateful}\:\boldsymbol{{sir}}\:\boldsymbol{{mr}}\:\boldsymbol{{W}}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *