Question Number 148947 by mathdanisur last updated on 01/Aug/21
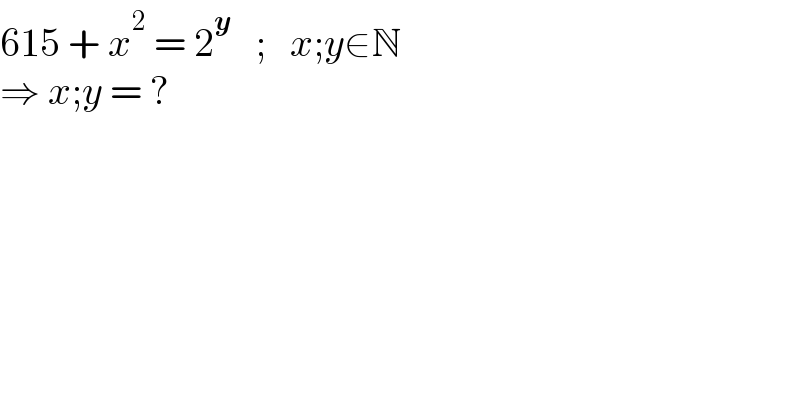
$$\mathrm{615}\:+\:{x}^{\mathrm{2}} \:=\:\mathrm{2}^{\boldsymbol{{y}}} \:\:\:;\:\:\:{x};{y}\in\mathbb{N} \\ $$$$\Rightarrow\:{x};{y}\:=\:? \\ $$
Answered by dumitrel last updated on 02/Aug/21
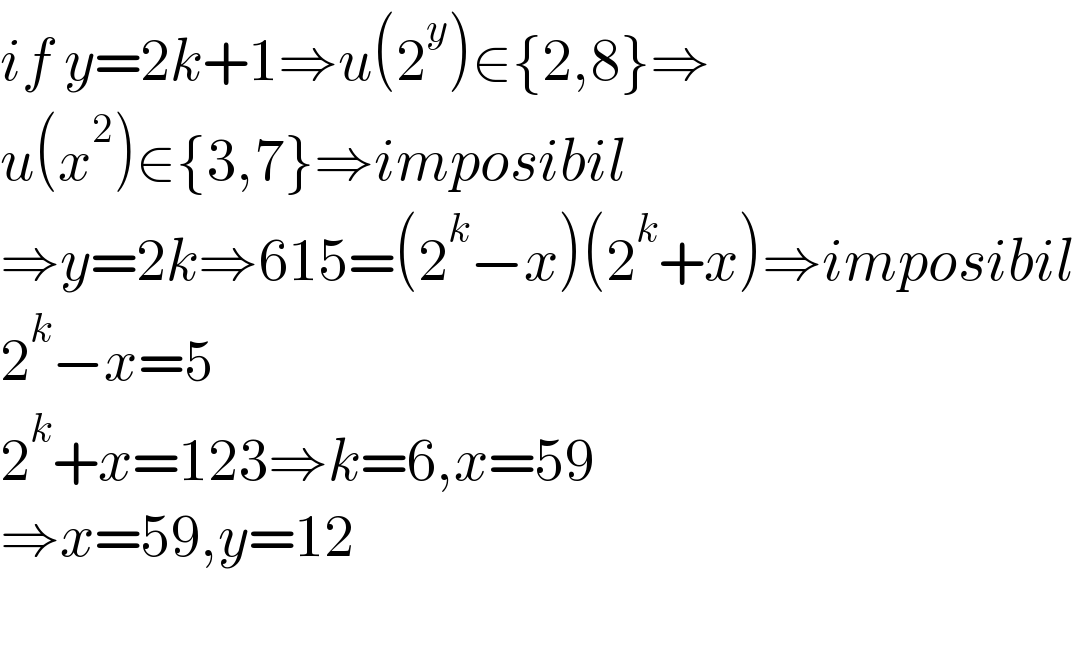
$${if}\:{y}=\mathrm{2}{k}+\mathrm{1}\Rightarrow{u}\left(\mathrm{2}^{{y}} \right)\in\left\{\mathrm{2},\mathrm{8}\right\}\Rightarrow \\ $$$${u}\left({x}^{\mathrm{2}} \right)\in\left\{\mathrm{3},\mathrm{7}\right\}\Rightarrow{imposibil} \\ $$$$\Rightarrow{y}=\mathrm{2}{k}\Rightarrow\mathrm{615}=\left(\mathrm{2}^{{k}} −{x}\right)\left(\mathrm{2}^{{k}} +{x}\right)\Rightarrow{imposibil} \\ $$$$\mathrm{2}^{{k}} −{x}=\mathrm{5} \\ $$$$\mathrm{2}^{{k}} +{x}=\mathrm{123}\Rightarrow{k}=\mathrm{6},{x}=\mathrm{59} \\ $$$$\Rightarrow{x}=\mathrm{59},{y}=\mathrm{12} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 01/Aug/21
$${Thank}\:{You}\:{Ser},\:{Cool} \\ $$
