Question Number 82881 by jagoll last updated on 25/Feb/20
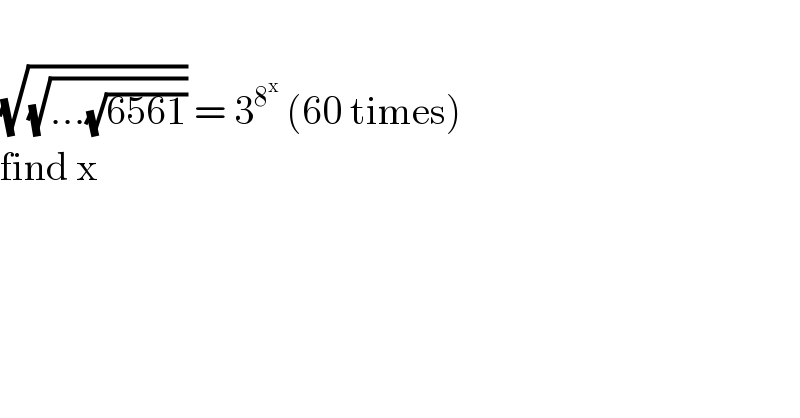
$$ \\ $$$$\sqrt{\sqrt{…\sqrt{\mathrm{6561}}}}\:=\:\mathrm{3}^{\mathrm{8}^{\mathrm{x}} } \:\left(\mathrm{60}\:\mathrm{times}\right) \\ $$$$\mathrm{find}\:\mathrm{x} \\ $$
Commented by mr W last updated on 25/Feb/20

$$\mathrm{6561}^{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{60}} } =\mathrm{3}^{\mathrm{8}^{{x}} } \\ $$$$\mathrm{3}^{\mathrm{8}×\frac{\mathrm{1}}{\mathrm{8}^{\mathrm{20}} }} =\mathrm{3}^{\mathrm{8}^{{x}} } \\ $$$$\mathrm{3}^{\mathrm{8}^{−\mathrm{19}} } =\mathrm{3}^{\mathrm{8}^{{x}} } \\ $$$$\Rightarrow{x}=−\mathrm{19} \\ $$
Commented by jagoll last updated on 25/Feb/20

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
Answered by john santu last updated on 25/Feb/20
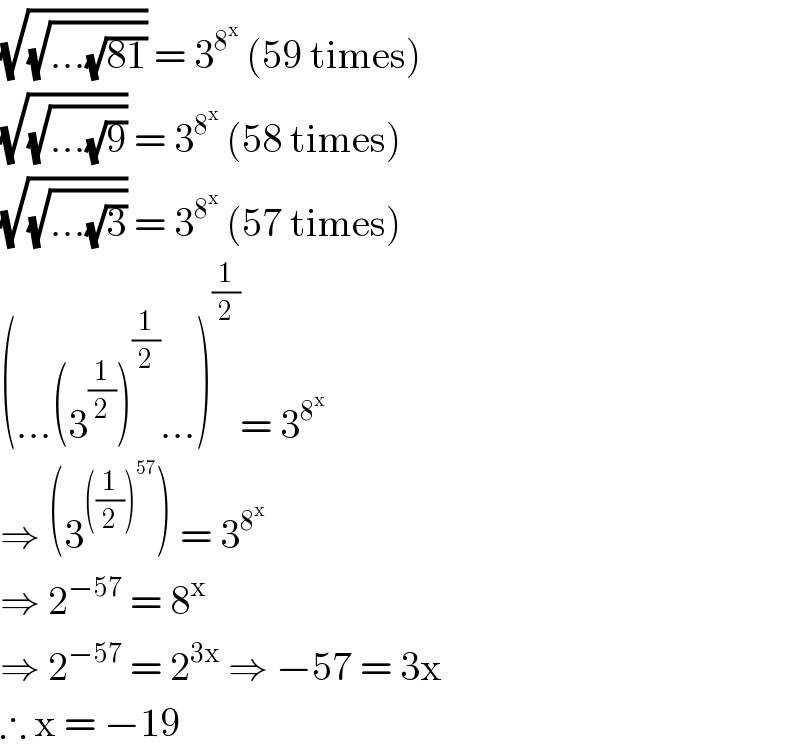
$$\sqrt{\sqrt{…\sqrt{\mathrm{81}}}}\:=\:\mathrm{3}^{\mathrm{8}^{\mathrm{x}} } \:\left(\mathrm{59}\:\mathrm{times}\right) \\ $$$$\sqrt{\sqrt{…\sqrt{\mathrm{9}}}}\:=\:\mathrm{3}^{\mathrm{8}^{\mathrm{x}} } \:\left(\mathrm{58}\:\mathrm{times}\right) \\ $$$$\sqrt{\sqrt{…\sqrt{\mathrm{3}}}}\:=\:\mathrm{3}^{\mathrm{8}^{\mathrm{x}} } \:\left(\mathrm{57}\:\mathrm{times}\right) \\ $$$$\left(…\left(\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} …\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\:\mathrm{3}^{\mathrm{8}^{\mathrm{x}} } \\ $$$$\Rightarrow\:\left(\mathrm{3}^{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{57}} } \right)\:=\:\mathrm{3}^{\mathrm{8}^{\mathrm{x}} } \\ $$$$\Rightarrow\:\mathrm{2}^{−\mathrm{57}} \:=\:\mathrm{8}^{\mathrm{x}} \: \\ $$$$\Rightarrow\:\mathrm{2}^{−\mathrm{57}} \:=\:\mathrm{2}^{\mathrm{3x}} \:\Rightarrow\:−\mathrm{57}\:=\:\mathrm{3x} \\ $$$$\therefore\:\mathrm{x}\:=\:−\mathrm{19} \\ $$
