Question Number 82665 by jagoll last updated on 23/Feb/20
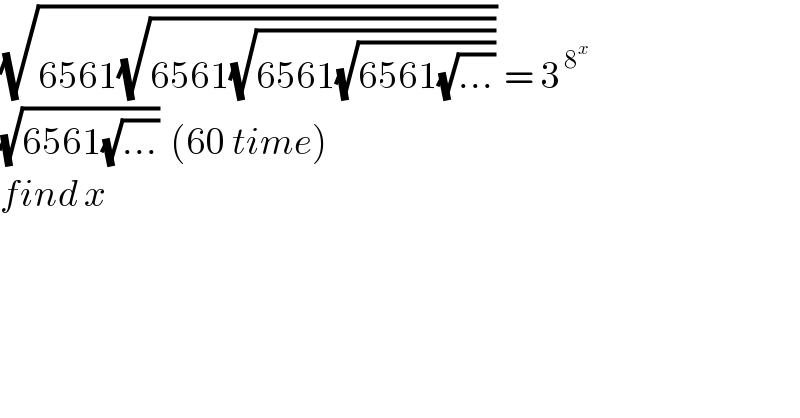
$$\sqrt{\mathrm{6561}\sqrt{\mathrm{6561}\sqrt{\mathrm{6561}\sqrt{\mathrm{6561}\sqrt{…}}}}}\:=\:\mathrm{3}^{\:\mathrm{8}^{{x}} \:} \\ $$$$\sqrt{\mathrm{6561}\sqrt{…}}\:\:\left(\mathrm{60}\:{time}\right) \\ $$$${find}\:{x} \\ $$
Commented by mr W last updated on 23/Feb/20
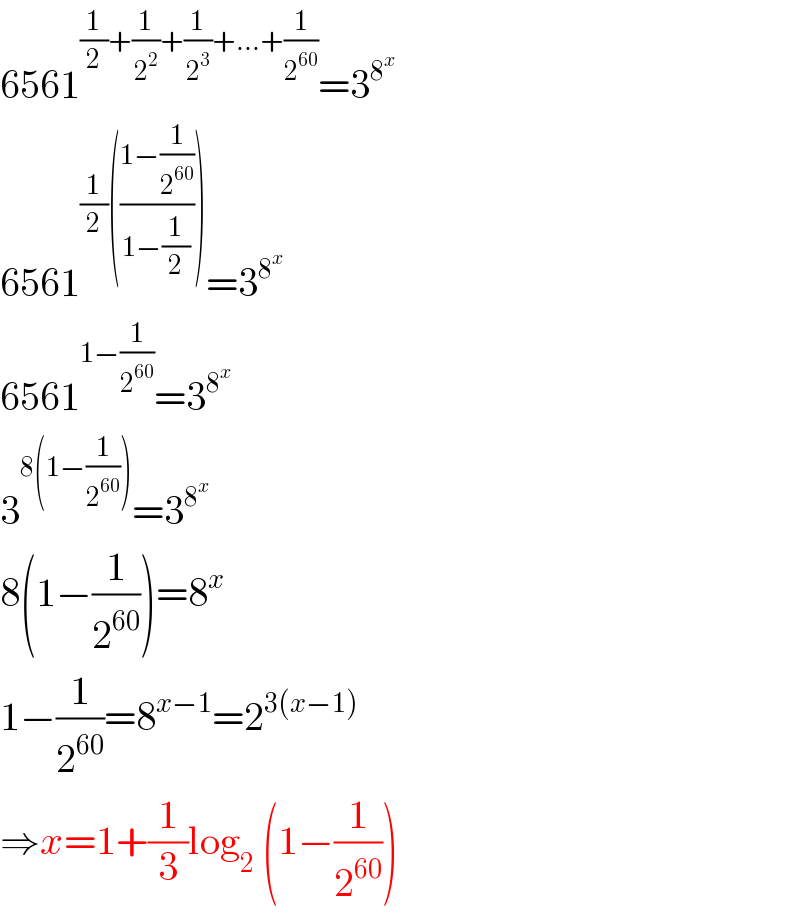
$$\mathrm{6561}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+…+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }} =\mathrm{3}^{\mathrm{8}^{{x}} } \\ $$$$\mathrm{6561}^{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\right)} =\mathrm{3}^{\mathrm{8}^{{x}} } \\ $$$$\mathrm{6561}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }} =\mathrm{3}^{\mathrm{8}^{{x}} } \\ $$$$\mathrm{3}^{\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }\right)} =\mathrm{3}^{\mathrm{8}^{{x}} } \\ $$$$\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }\right)=\mathrm{8}^{{x}} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }=\mathrm{8}^{{x}−\mathrm{1}} =\mathrm{2}^{\mathrm{3}\left({x}−\mathrm{1}\right)} \\ $$$$\Rightarrow{x}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }\right) \\ $$
Commented by jagoll last updated on 23/Feb/20
$${thank}\:{you}\:{mister}\:{w}\:{and}\:{mister}\:{john} \\ $$
Answered by john santu last updated on 23/Feb/20
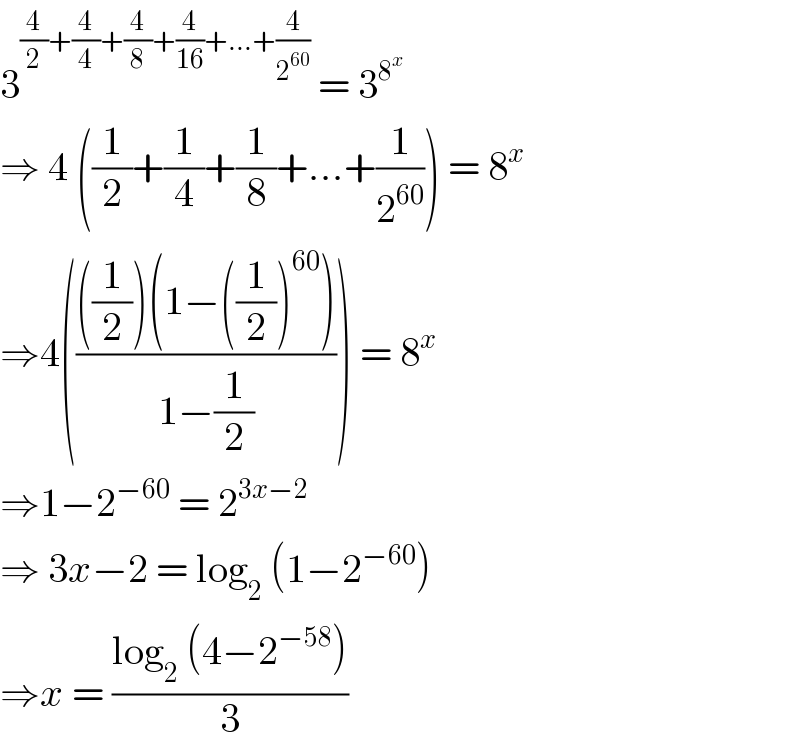
$$\mathrm{3}^{\frac{\mathrm{4}}{\mathrm{2}}+\frac{\mathrm{4}}{\mathrm{4}}+\frac{\mathrm{4}}{\mathrm{8}}+\frac{\mathrm{4}}{\mathrm{16}}+…+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{60}} }} \:=\:\mathrm{3}^{\mathrm{8}^{{x}\:} } \\ $$$$\Rightarrow\:\mathrm{4}\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}+…+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }\right)\:=\:\mathrm{8}^{{x}} \\ $$$$\Rightarrow\mathrm{4}\left(\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{60}} \right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\right)\:=\:\mathrm{8}^{{x}} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2}^{−\mathrm{60}} \:=\:\mathrm{2}^{\mathrm{3}{x}−\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{3}{x}−\mathrm{2}\:=\:\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{1}−\mathrm{2}^{−\mathrm{60}} \right) \\ $$$$\Rightarrow{x}\:=\:\frac{\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{4}−\mathrm{2}^{−\mathrm{58}} \right)}{\mathrm{3}} \\ $$
