Menu Close

69x-1-mod-31-solve-for-x-

Tinku Tara 0 Comments
Pin




Question Number 96928 by bobhans last updated on 05/Jun/20
69x ≡ 1 (mod 31) solve for x
$$\mathrm{69}{x}\:\equiv\:\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{31}\right)\: \\ $$$$\mathrm{solve}\:\mathrm{for}\:{x} \\ $$
Commented by RAMANA last updated on 05/Jun/20
send the answer please
$${send}\:{the}\:{answer}\:{please} \\ $$
Answered by MAB last updated on 05/Jun/20
69x≡1[31] 69x−31×2×x≡1[31] 7x≡1[31] we have 31 is prime and 7x≡1[31] and the only inverse of 7 in the class 31 is 9 ( 7×9=63=2×31+1) therfore x≡ [31]
$$\mathrm{69}{x}\equiv\mathrm{1}\left[\mathrm{31}\right] \\ $$$$\mathrm{69}{x}−\mathrm{31}×\mathrm{2}×{x}\equiv\mathrm{1}\left[\mathrm{31}\right] \\ $$$$\mathrm{7}{x}\equiv\mathrm{1}\left[\mathrm{31}\right] \\ $$$${we}\:{have}\:\mathrm{31}\:{is}\:{prime}\:{and}\:\mathrm{7}{x}\equiv\mathrm{1}\left[\mathrm{31}\right]\: \\ $$$${and}\:{the}\:{only}\:{inverse}\:{of}\:\mathrm{7}\:{in}\:{the}\:{class}\:\mathrm{31} \\ $$$${is}\:\mathrm{9}\:\left(\:\mathrm{7}×\mathrm{9}=\mathrm{63}=\mathrm{2}×\mathrm{31}+\mathrm{1}\right) \\ $$$${therfore}\:{x}\equiv\:\left[\mathrm{31}\right] \\ $$
Answered by 1549442205 last updated on 06/Jun/20
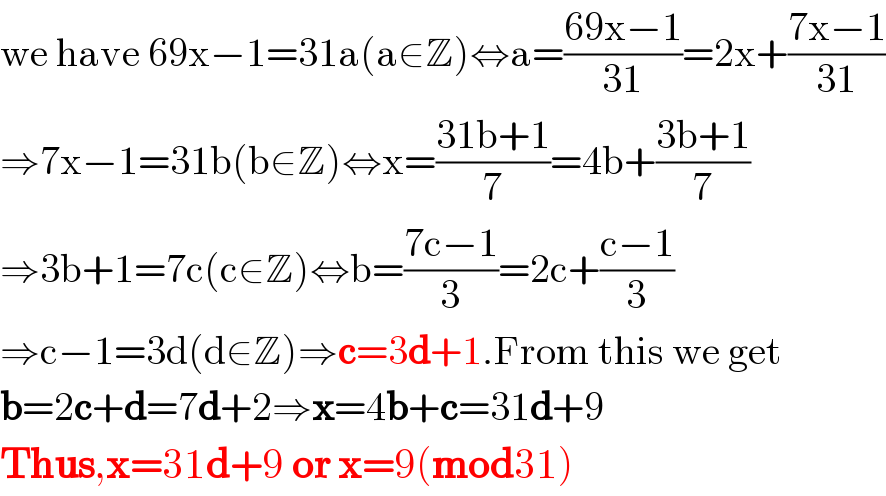
we have 69x−1=31a(a∈Z)⇔a=((69x−1)/(31))=2x+((7x−1)/(31)) ⇒7x−1=31b(b∈Z)⇔x=((31b+1)/7)=4b+((3b+1)/7) ⇒3b+1=7c(c∈Z)⇔b=((7c−1)/3)=2c+((c−1)/3) ⇒c−1=3d(d∈Z)⇒c=3d+1.From this we get b=2c+d=7d+2⇒x=4b+c=31d+9 Thus,x=31d+9 or x=9(mod31)
$$\mathrm{we}\:\mathrm{have}\:\mathrm{69x}−\mathrm{1}=\mathrm{31a}\left(\mathrm{a}\in\mathbb{Z}\right)\Leftrightarrow\mathrm{a}=\frac{\mathrm{69x}−\mathrm{1}}{\mathrm{31}}=\mathrm{2x}+\frac{\mathrm{7x}−\mathrm{1}}{\mathrm{31}} \\ $$$$\Rightarrow\mathrm{7x}−\mathrm{1}=\mathrm{31b}\left(\mathrm{b}\in\mathbb{Z}\right)\Leftrightarrow\mathrm{x}=\frac{\mathrm{31b}+\mathrm{1}}{\mathrm{7}}=\mathrm{4b}+\frac{\mathrm{3b}+\mathrm{1}}{\mathrm{7}} \\ $$$$\Rightarrow\mathrm{3b}+\mathrm{1}=\mathrm{7c}\left(\mathrm{c}\in\mathbb{Z}\right)\Leftrightarrow\mathrm{b}=\frac{\mathrm{7c}−\mathrm{1}}{\mathrm{3}}=\mathrm{2c}+\frac{\mathrm{c}−\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{c}−\mathrm{1}=\mathrm{3d}\left(\mathrm{d}\in\mathbb{Z}\right)\Rightarrow\boldsymbol{\mathrm{c}}=\mathrm{3}\boldsymbol{\mathrm{d}}+\mathrm{1}.\mathrm{From}\:\mathrm{this}\:\mathrm{we}\:\mathrm{get} \\ $$$$\boldsymbol{\mathrm{b}}=\mathrm{2}\boldsymbol{\mathrm{c}}+\boldsymbol{\mathrm{d}}=\mathrm{7}\boldsymbol{\mathrm{d}}+\mathrm{2}\Rightarrow\boldsymbol{\mathrm{x}}=\mathrm{4}\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{c}}=\mathrm{31}\boldsymbol{\mathrm{d}}+\mathrm{9} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{x}}=\mathrm{31}\boldsymbol{\mathrm{d}}+\mathrm{9}\:\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{x}}=\mathrm{9}\left(\boldsymbol{\mathrm{mod}}\mathrm{31}\right) \\ $$
Answered by mr W last updated on 06/Jun/20
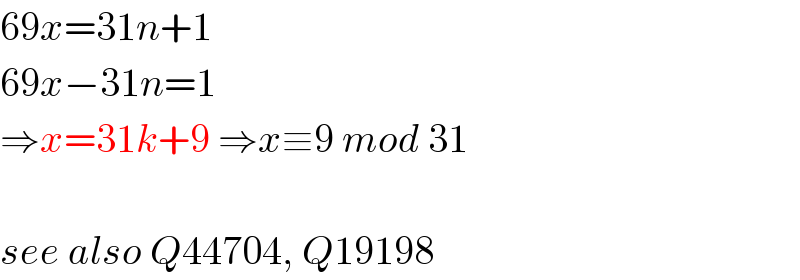
69x=31n+1 69x−31n=1 ⇒x=31k+9 ⇒x≡9 mod 31 see also Q44704, Q19198
$$\mathrm{69}{x}=\mathrm{31}{n}+\mathrm{1} \\ $$$$\mathrm{69}{x}−\mathrm{31}{n}=\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{31}{k}+\mathrm{9}\:\Rightarrow{x}\equiv\mathrm{9}\:{mod}\:\mathrm{31} \\ $$$$ \\ $$$${see}\:{also}\:{Q}\mathrm{44704},\:{Q}\mathrm{19198} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *