Question Number 86998 by M±th+et£s last updated on 01/Apr/20

$$\int\frac{\mathrm{6}{e}^{{x}} }{{e}^{\mathrm{2}{x}} −\mathrm{1}}\:{dx} \\ $$
Answered by TANMAY PANACEA. last updated on 01/Apr/20
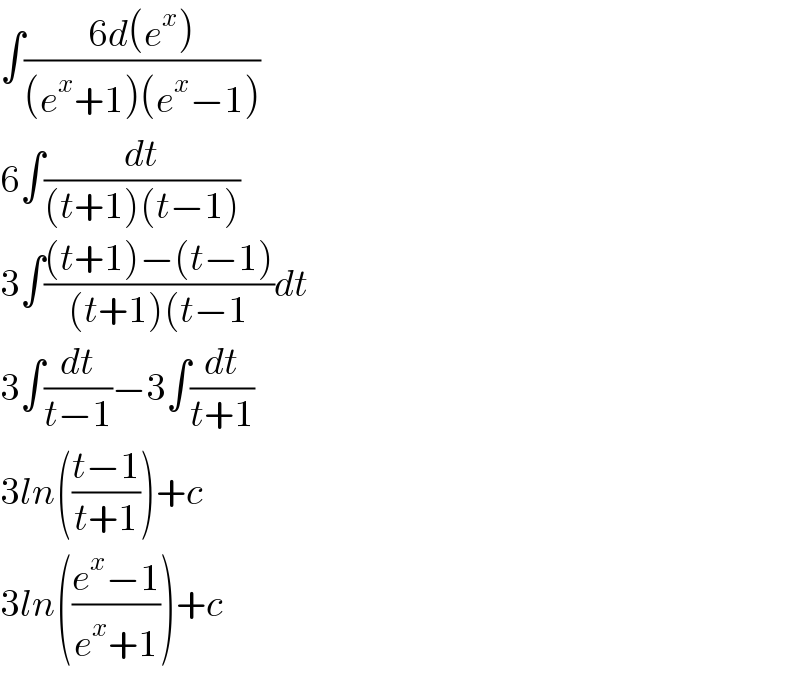
$$\int\frac{\mathrm{6}{d}\left({e}^{{x}} \right)}{\left({e}^{{x}} +\mathrm{1}\right)\left({e}^{{x}} −\mathrm{1}\right)} \\ $$$$\mathrm{6}\int\frac{{dt}}{\left({t}+\mathrm{1}\right)\left({t}−\mathrm{1}\right)} \\ $$$$\mathrm{3}\int\frac{\left({t}+\mathrm{1}\right)−\left({t}−\mathrm{1}\right)}{\left({t}+\mathrm{1}\right)\left({t}−\mathrm{1}\right.}{dt} \\ $$$$\mathrm{3}\int\frac{{dt}}{{t}−\mathrm{1}}−\mathrm{3}\int\frac{{dt}}{{t}+\mathrm{1}} \\ $$$$\mathrm{3}{ln}\left(\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\right)+{c} \\ $$$$\mathrm{3}{ln}\left(\frac{{e}^{{x}} −\mathrm{1}}{{e}^{{x}} +\mathrm{1}}\right)+{c} \\ $$
