Question Number 58092 by smiak8742 last updated on 17/Apr/19
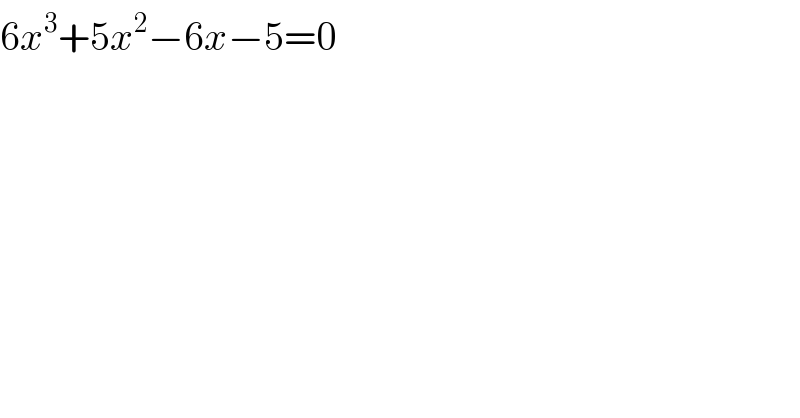
$$\mathrm{6}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{5}=\mathrm{0} \\ $$
Answered by tanmay last updated on 17/Apr/19
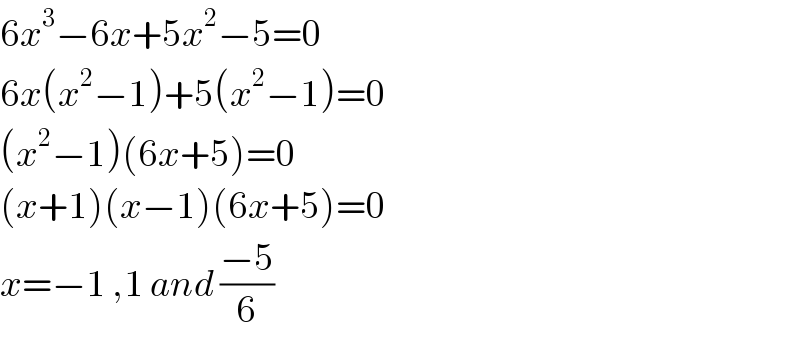
$$\mathrm{6}{x}^{\mathrm{3}} −\mathrm{6}{x}+\mathrm{5}{x}^{\mathrm{2}} −\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{6}{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{5}\left({x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{6}{x}+\mathrm{5}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)\left(\mathrm{6}{x}+\mathrm{5}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{1}\:,\mathrm{1}\:{and}\:\frac{−\mathrm{5}}{\mathrm{6}} \\ $$
Answered by Kunal12588 last updated on 17/Apr/19
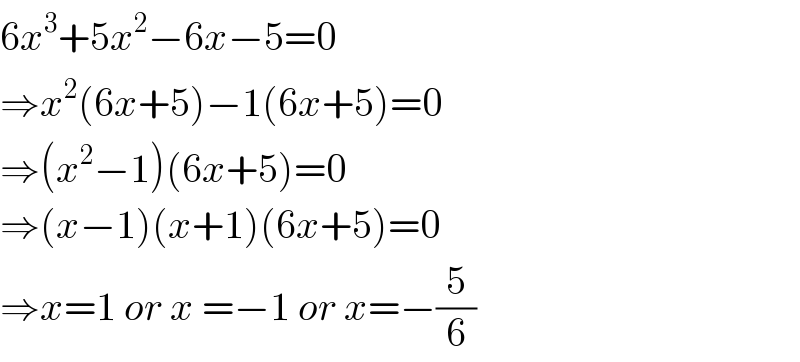
$$\mathrm{6}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left(\mathrm{6}{x}+\mathrm{5}\right)−\mathrm{1}\left(\mathrm{6}{x}+\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{6}{x}+\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)\left(\mathrm{6}{x}+\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{1}\:{or}\:{x}\:=−\mathrm{1}\:{or}\:{x}=−\frac{\mathrm{5}}{\mathrm{6}} \\ $$
Answered by MJS last updated on 17/Apr/19
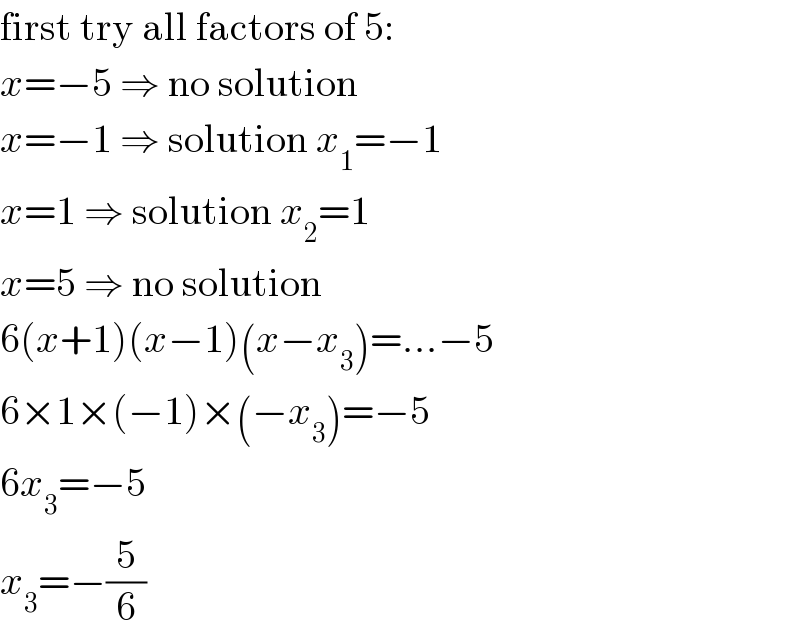
$$\mathrm{first}\:\mathrm{try}\:\mathrm{all}\:\mathrm{factors}\:\mathrm{of}\:\mathrm{5}: \\ $$$${x}=−\mathrm{5}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$${x}=−\mathrm{1}\:\Rightarrow\:\mathrm{solution}\:{x}_{\mathrm{1}} =−\mathrm{1} \\ $$$${x}=\mathrm{1}\:\Rightarrow\:\mathrm{solution}\:{x}_{\mathrm{2}} =\mathrm{1} \\ $$$${x}=\mathrm{5}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{6}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)\left({x}−{x}_{\mathrm{3}} \right)=…−\mathrm{5} \\ $$$$\mathrm{6}×\mathrm{1}×\left(−\mathrm{1}\right)×\left(−{x}_{\mathrm{3}} \right)=−\mathrm{5} \\ $$$$\mathrm{6}{x}_{\mathrm{3}} =−\mathrm{5} \\ $$$${x}_{\mathrm{3}} =−\frac{\mathrm{5}}{\mathrm{6}} \\ $$
