Question Number 165562 by cortano1 last updated on 04/Feb/22
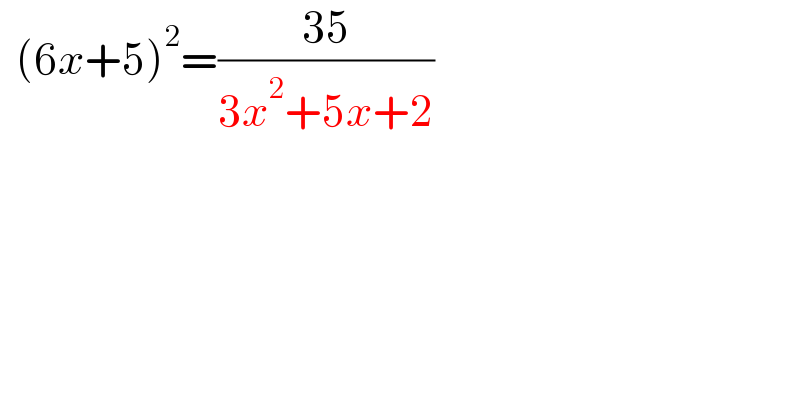
$$\:\:\left(\mathrm{6}{x}+\mathrm{5}\right)^{\mathrm{2}} =\frac{\mathrm{35}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{2}} \\ $$
Answered by som(math1967) last updated on 04/Feb/22
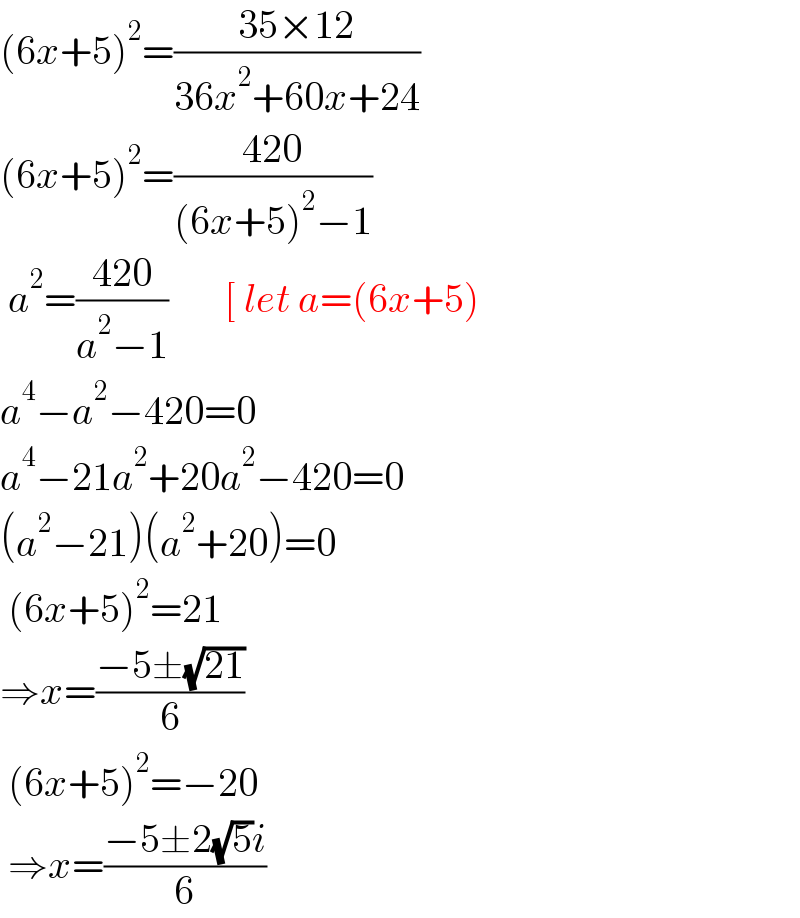
$$\left(\mathrm{6}{x}+\mathrm{5}\right)^{\mathrm{2}} =\frac{\mathrm{35}×\mathrm{12}}{\mathrm{36}{x}^{\mathrm{2}} +\mathrm{60}{x}+\mathrm{24}} \\ $$$$\left(\mathrm{6}{x}+\mathrm{5}\right)^{\mathrm{2}} =\frac{\mathrm{420}}{\left(\mathrm{6}{x}+\mathrm{5}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:{a}^{\mathrm{2}} =\frac{\mathrm{420}}{{a}^{\mathrm{2}} −\mathrm{1}}\:\:\:\:\:\:\:\left[\:{let}\:{a}=\left(\mathrm{6}{x}+\mathrm{5}\right)\right. \\ $$$${a}^{\mathrm{4}} −{a}^{\mathrm{2}} −\mathrm{420}=\mathrm{0} \\ $$$${a}^{\mathrm{4}} −\mathrm{21}{a}^{\mathrm{2}} +\mathrm{20}{a}^{\mathrm{2}} −\mathrm{420}=\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} −\mathrm{21}\right)\left({a}^{\mathrm{2}} +\mathrm{20}\right)=\mathrm{0} \\ $$$$\:\left(\mathrm{6}{x}+\mathrm{5}\right)^{\mathrm{2}} =\mathrm{21} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{5}\pm\sqrt{\mathrm{21}}}{\mathrm{6}} \\ $$$$\:\left(\mathrm{6}{x}+\mathrm{5}\right)^{\mathrm{2}} =−\mathrm{20} \\ $$$$\:\Rightarrow{x}=\frac{−\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{5}}{i}}{\mathrm{6}} \\ $$
Commented by cortano1 last updated on 04/Feb/22

$${nice} \\ $$
