Question Number 124050 by john_santu last updated on 30/Nov/20
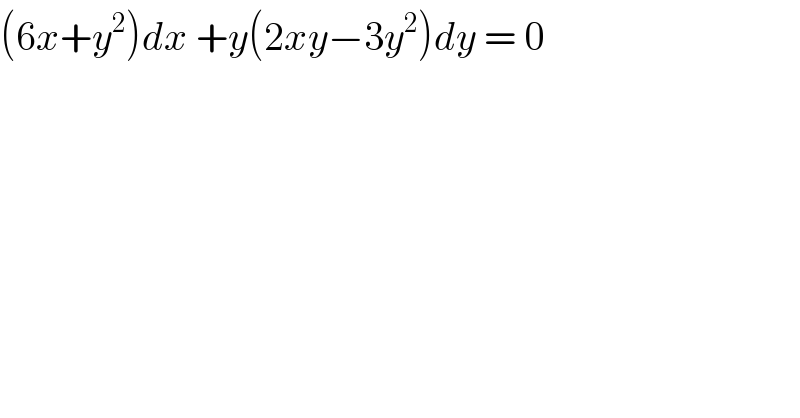
$$\left(\mathrm{6}{x}+{y}^{\mathrm{2}} \right){dx}\:+{y}\left(\mathrm{2}{xy}−\mathrm{3}{y}^{\mathrm{2}} \right){dy}\:=\:\mathrm{0}\: \\ $$
Answered by mohammad17 last updated on 30/Nov/20
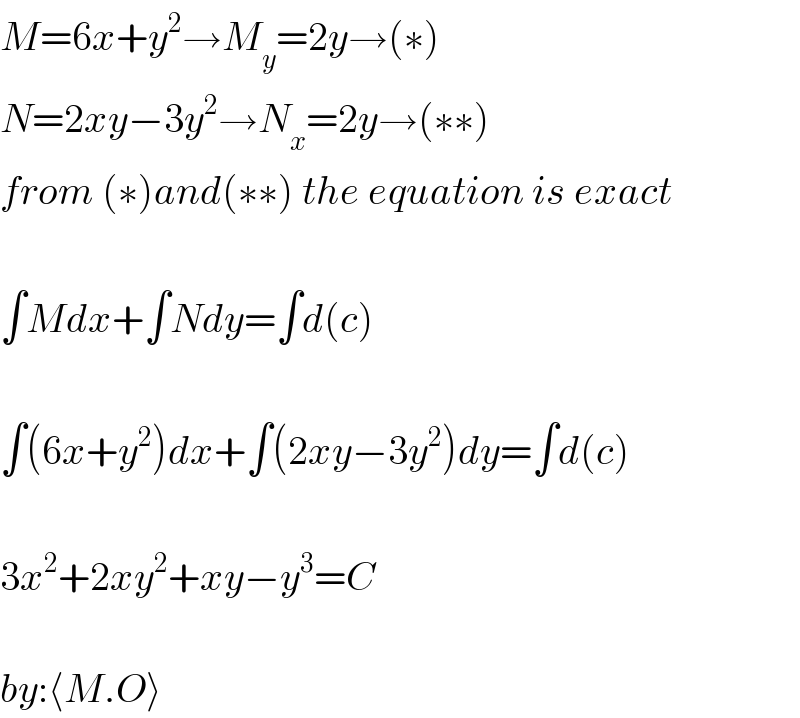
$${M}=\mathrm{6}{x}+{y}^{\mathrm{2}} \rightarrow{M}_{{y}} =\mathrm{2}{y}\rightarrow\left(\ast\right) \\ $$$${N}=\mathrm{2}{xy}−\mathrm{3}{y}^{\mathrm{2}} \rightarrow{N}_{{x}} =\mathrm{2}{y}\rightarrow\left(\ast\ast\right) \\ $$$${from}\:\left(\ast\right){and}\left(\ast\ast\right)\:{the}\:{equation}\:{is}\:{exact} \\ $$$$ \\ $$$$\int{Mdx}+\int{Ndy}=\int{d}\left({c}\right) \\ $$$$ \\ $$$$\int\left(\mathrm{6}{x}+{y}^{\mathrm{2}} \right){dx}+\int\left(\mathrm{2}{xy}−\mathrm{3}{y}^{\mathrm{2}} \right){dy}=\int{d}\left({c}\right) \\ $$$$ \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{xy}^{\mathrm{2}} +{xy}−{y}^{\mathrm{3}} ={C} \\ $$$$ \\ $$$${by}:\langle{M}.{O}\rangle \\ $$
