Question Number 160165 by cortano last updated on 25/Nov/21
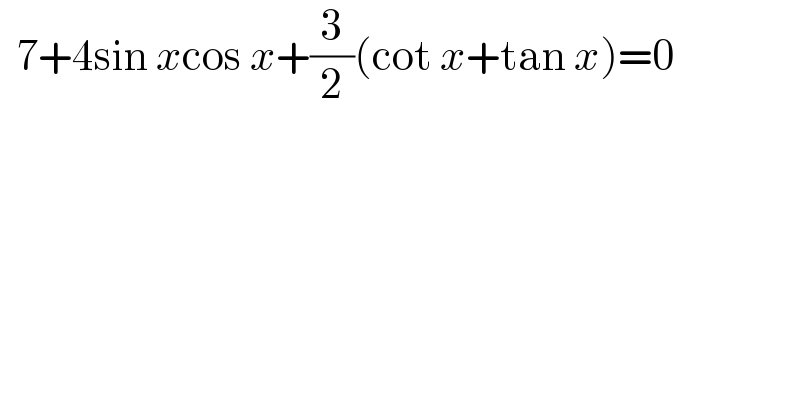
$$\:\:\mathrm{7}+\mathrm{4sin}\:{x}\mathrm{cos}\:{x}+\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{cot}\:{x}+\mathrm{tan}\:{x}\right)=\mathrm{0}\: \\ $$
Commented by cortano last updated on 25/Nov/21

Answered by som(math1967) last updated on 25/Nov/21

$$\mathrm{7}+\mathrm{2}.\mathrm{2}{sinxcosx}+\frac{\mathrm{3}\left({sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}\right)}{\mathrm{2}{sinxcosx}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{7}+\mathrm{2}{sin}\mathrm{2}{x}+\frac{\mathrm{3}}{{sin}\mathrm{2}{x}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{sin}^{\mathrm{2}} \mathrm{2}{x}+\mathrm{7}{sin}\mathrm{2}{x}+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{sin}\mathrm{2}{x}+\mathrm{1}\right)\left({sin}\mathrm{2}{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow{sin}\mathrm{2}{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{x}={n}\pi+\left(−\mathrm{1}\right)^{{n}} \left(−\frac{\pi}{\mathrm{6}}\right) \\ $$$$\:{x}=\frac{{n}\pi}{\mathrm{2}}\:+\left(−\mathrm{1}\right)^{{n}} \left(−\frac{\pi}{\mathrm{12}}\right)\:\boldsymbol{{n}}\in{Z} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Nov/21

$$\cap\mathrm{i}\subset\in! \\ $$
Commented by som(math1967) last updated on 25/Nov/21

$${if}\:{x}=−\frac{\pi}{\mathrm{4}}\:{then}\:{equation}\:{is}\:{satisfied}\:? \\ $$
