Question Number 157441 by bobhans last updated on 23/Oct/21
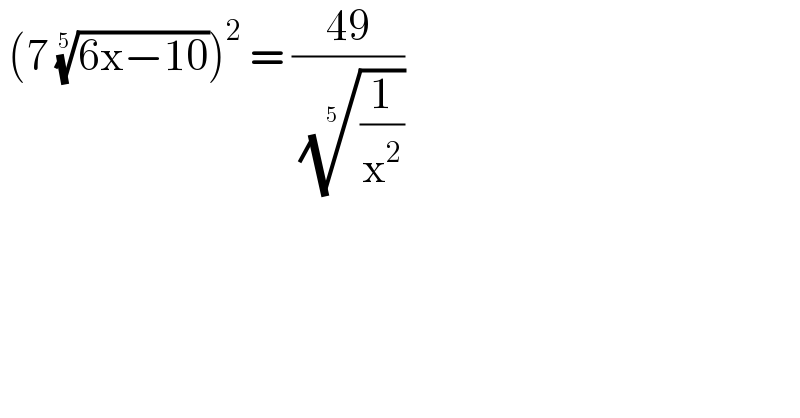
$$\:\left(\mathrm{7}\:\sqrt[{\mathrm{5}}]{\mathrm{6x}−\mathrm{10}}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{49}}{\:\sqrt[{\mathrm{5}}]{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}}\: \\ $$
Answered by MJS_new last updated on 23/Oct/21

$$\mathrm{49}\left(\mathrm{6}{x}−\mathrm{10}\right)^{\mathrm{2}/\mathrm{5}} =\mathrm{49}{x}^{\mathrm{2}/\mathrm{5}} \\ $$$$\left(\mathrm{6}{x}−\mathrm{10}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{24}}{\mathrm{7}}{x}+\frac{\mathrm{20}}{\mathrm{7}}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{10}}{\mathrm{7}}\vee{x}=\mathrm{2} \\ $$
Answered by cortano last updated on 23/Oct/21
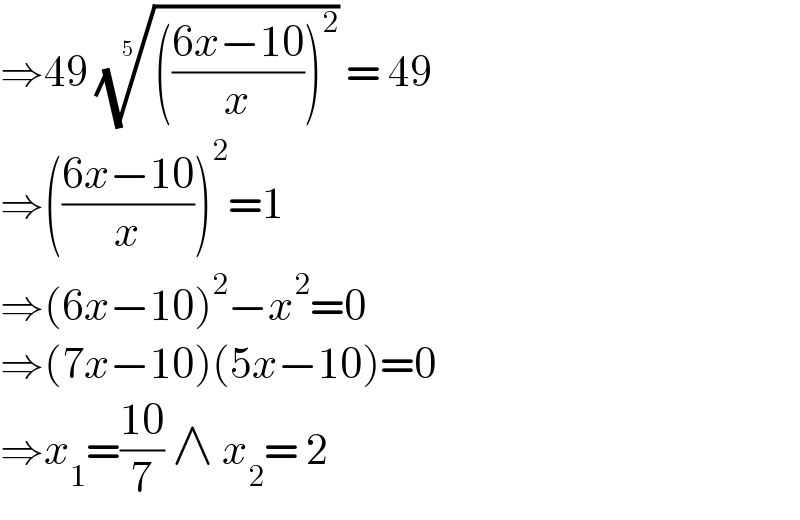
$$\Rightarrow\mathrm{49}\:\sqrt[{\mathrm{5}}]{\left(\frac{\mathrm{6}{x}−\mathrm{10}}{{x}}\right)^{\mathrm{2}} }\:=\:\mathrm{49} \\ $$$$\Rightarrow\left(\frac{\mathrm{6}{x}−\mathrm{10}}{{x}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{6}{x}−\mathrm{10}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{7}{x}−\mathrm{10}\right)\left(\mathrm{5}{x}−\mathrm{10}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{10}}{\mathrm{7}}\:\wedge\:{x}_{\mathrm{2}} =\:\mathrm{2} \\ $$
