Question Number 92279 by M±th+et+s last updated on 06/May/20
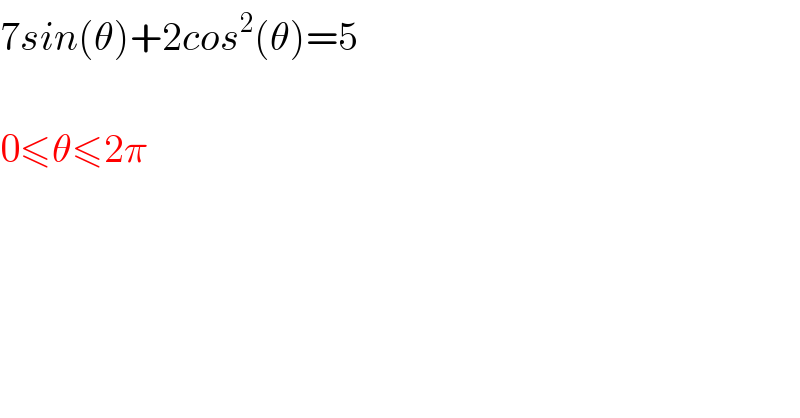
$$\mathrm{7}{sin}\left(\theta\right)+\mathrm{2}{cos}^{\mathrm{2}} \left(\theta\right)=\mathrm{5} \\ $$$$ \\ $$$$\mathrm{0}\leqslant\theta\leqslant\mathrm{2}\pi \\ $$
Commented by jagoll last updated on 06/May/20
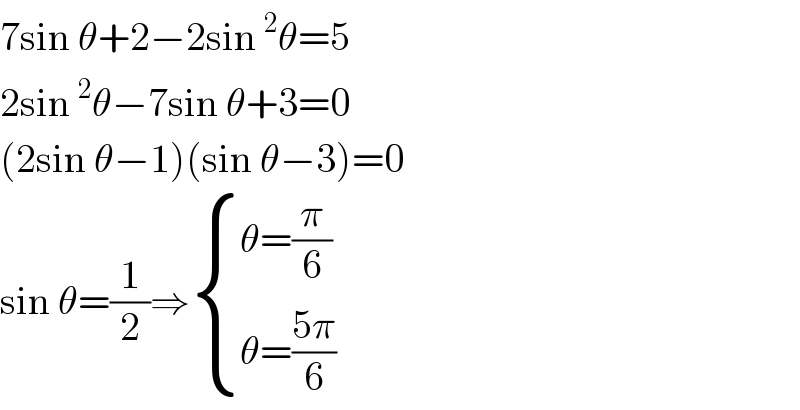
$$\mathrm{7sin}\:\theta+\mathrm{2}−\mathrm{2sin}\:^{\mathrm{2}} \theta=\mathrm{5} \\ $$$$\mathrm{2sin}\:^{\mathrm{2}} \theta−\mathrm{7sin}\:\theta+\mathrm{3}=\mathrm{0} \\ $$$$\left(\mathrm{2sin}\:\theta−\mathrm{1}\right)\left(\mathrm{sin}\:\theta−\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\begin{cases}{\theta=\frac{\pi}{\mathrm{6}}}\\{\theta=\frac{\mathrm{5}\pi}{\mathrm{6}}}\end{cases} \\ $$
Commented by M±th+et+s last updated on 06/May/20
correct solution thank you����
