Menu Close

8-1-1-2-1-1-2-2-1-1-2-4-1-1-2-8-1-1-2-32-1-2-60-

Tinku Tara 0 Comments
Pin




Question Number 118880 by bemath last updated on 20/Oct/20
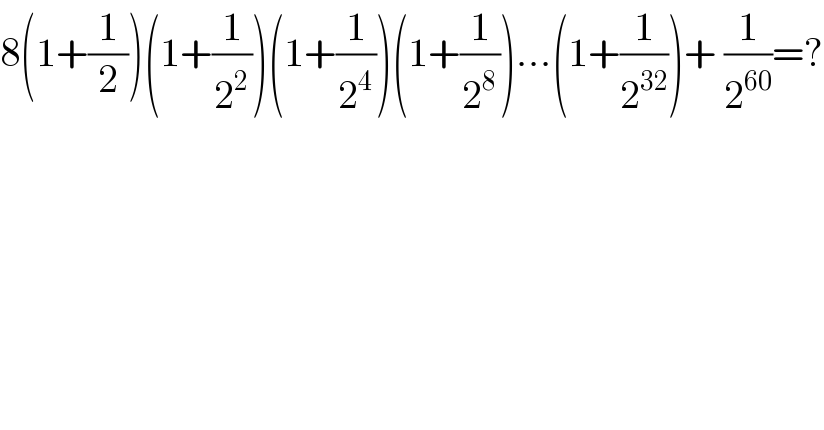
8(1+(1/2))(1+(1/2^2 ))(1+(1/2^4 ))(1+(1/2^8 ))...(1+(1/2^(32) ))+ (1/2^(60) )=?
$$\mathrm{8}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{8}} }\right)…\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }=? \\ $$
Answered by Dwaipayan Shikari last updated on 20/Oct/20
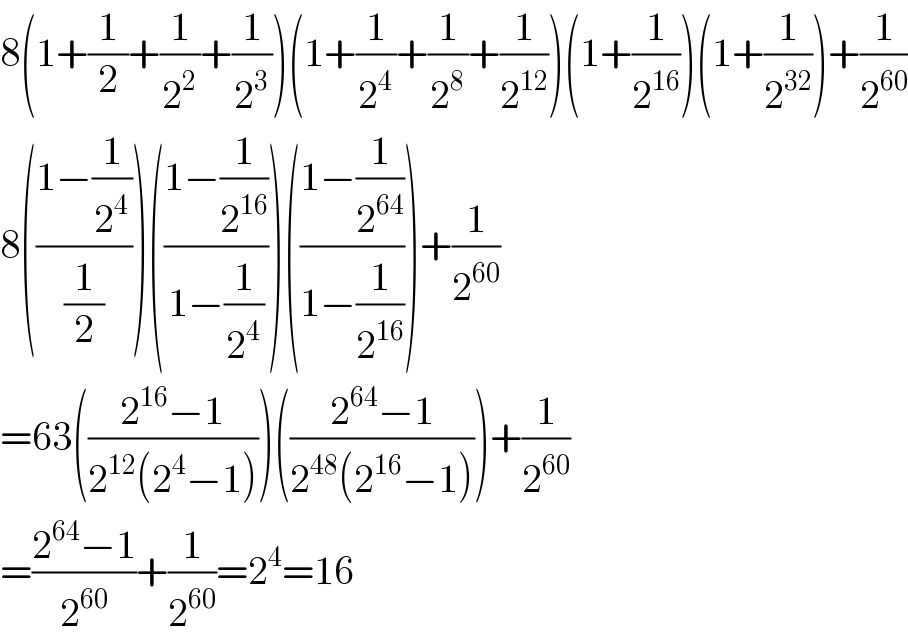
8(1+(1/2)+(1/2^2 )+(1/2^3 ))(1+(1/2^4 )+(1/2^8 )+(1/2^(12) ))(1+(1/2^(16) ))(1+(1/2^(32) ))+(1/2^(60) ) 8(((1−(1/2^4 ))/(1/2)))(((1−(1/2^(16) ))/(1−(1/2^4 ))))(((1−(1/2^(64) ))/(1−(1/2^(16) ))))+(1/2^(60) ) =63(((2^(16) −1)/(2^(12) (2^4 −1))))(((2^(64) −1)/(2^(48) (2^(16) −1))))+(1/2^(60) ) =((2^(64) −1)/2^(60) )+(1/2^(60) )=2^4 =16
$$\mathrm{8}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{8}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{12}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{16}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} } \\ $$$$\mathrm{8}\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }}{\frac{\mathrm{1}}{\mathrm{2}}}\right)\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{16}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }}\right)\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{64}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{16}} }}\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} } \\ $$$$=\mathrm{63}\left(\frac{\mathrm{2}^{\mathrm{16}} −\mathrm{1}}{\mathrm{2}^{\mathrm{12}} \left(\mathrm{2}^{\mathrm{4}} −\mathrm{1}\right)}\right)\left(\frac{\mathrm{2}^{\mathrm{64}} −\mathrm{1}}{\mathrm{2}^{\mathrm{48}} \left(\mathrm{2}^{\mathrm{16}} −\mathrm{1}\right)}\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} } \\ $$$$=\frac{\mathrm{2}^{\mathrm{64}} −\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }=\mathrm{2}^{\mathrm{4}} =\mathrm{16} \\ $$
Answered by bobhans last updated on 20/Oct/20
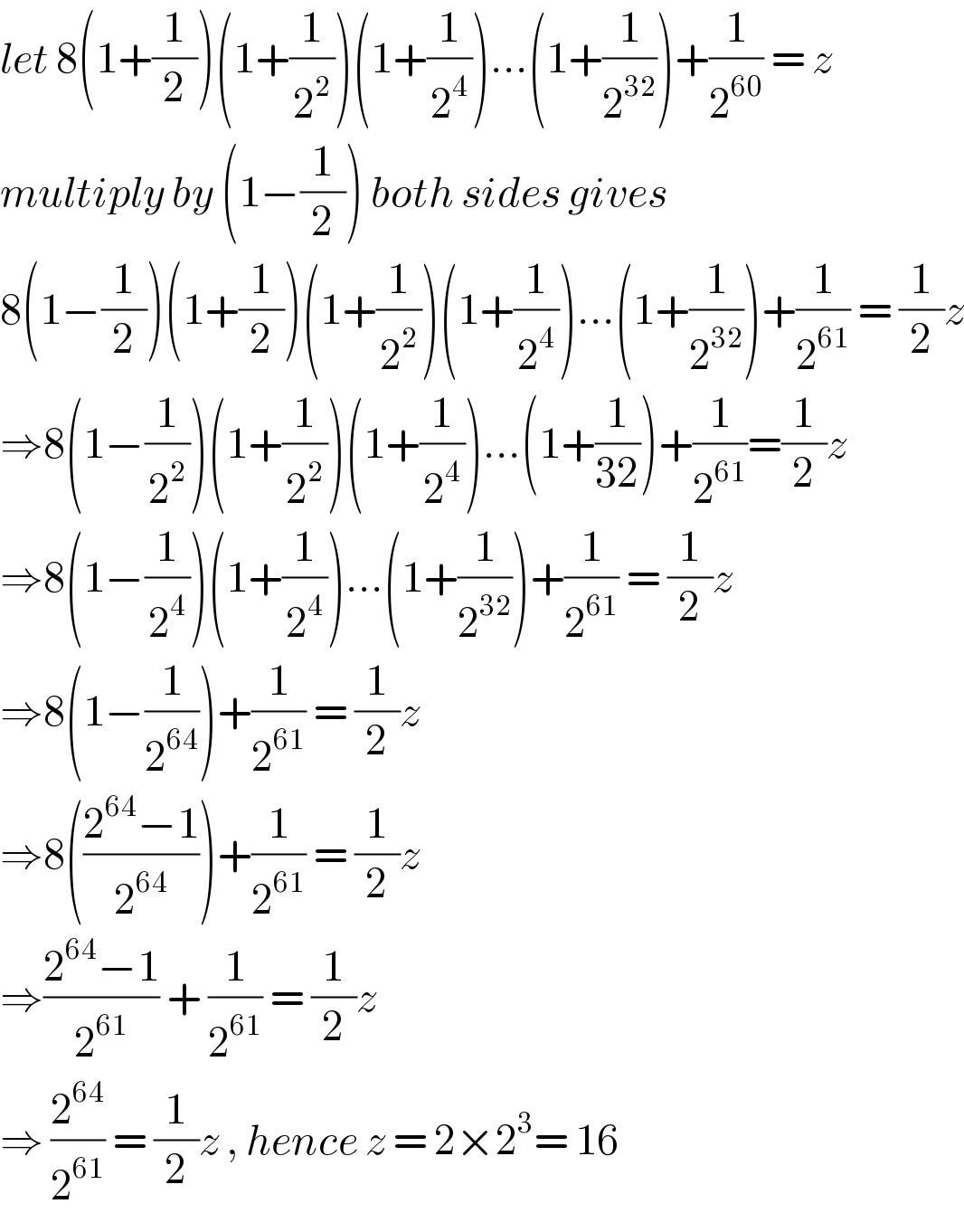
let 8(1+(1/2))(1+(1/2^2 ))(1+(1/2^4 ))...(1+(1/2^(32) ))+(1/2^(60) ) = z multiply by (1−(1/2)) both sides gives 8(1−(1/2))(1+(1/2))(1+(1/2^2 ))(1+(1/2^4 ))...(1+(1/2^(32) ))+(1/2^(61) ) = (1/2)z ⇒8(1−(1/2^2 ))(1+(1/2^2 ))(1+(1/2^4 ))...(1+(1/(32)))+(1/2^(61) )=(1/2)z ⇒8(1−(1/2^4 ))(1+(1/2^4 ))...(1+(1/2^(32) ))+(1/2^(61) ) = (1/2)z ⇒8(1−(1/2^(64) ))+(1/2^(61) ) = (1/2)z ⇒8(((2^(64) −1)/2^(64) ))+(1/2^(61) ) = (1/2)z ⇒((2^(64) −1)/2^(61) ) + (1/2^(61) ) = (1/2)z ⇒ (2^(64) /2^(61) ) = (1/2)z , hence z = 2×2^3 = 16
$${let}\:\mathrm{8}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)…\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{60}} }\:=\:{z} \\ $$$${multiply}\:{by}\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:{both}\:{sides}\:{gives} \\ $$$$\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)…\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}{z} \\ $$$$\Rightarrow\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)…\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{32}}\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }=\frac{\mathrm{1}}{\mathrm{2}}{z} \\ $$$$\Rightarrow\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)…\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}{z} \\ $$$$\Rightarrow\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{64}} }\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}{z} \\ $$$$\Rightarrow\mathrm{8}\left(\frac{\mathrm{2}^{\mathrm{64}} −\mathrm{1}}{\mathrm{2}^{\mathrm{64}} }\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}{z}\: \\ $$$$\Rightarrow\frac{\mathrm{2}^{\mathrm{64}} −\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}{z}\: \\ $$$$\Rightarrow\:\frac{\mathrm{2}^{\mathrm{64}} }{\mathrm{2}^{\mathrm{61}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}{z}\:,\:{hence}\:{z}\:=\:\mathrm{2}×\mathrm{2}^{\mathrm{3}} =\:\mathrm{16} \\ $$
Answered by 1549442205PVT last updated on 21/Oct/20
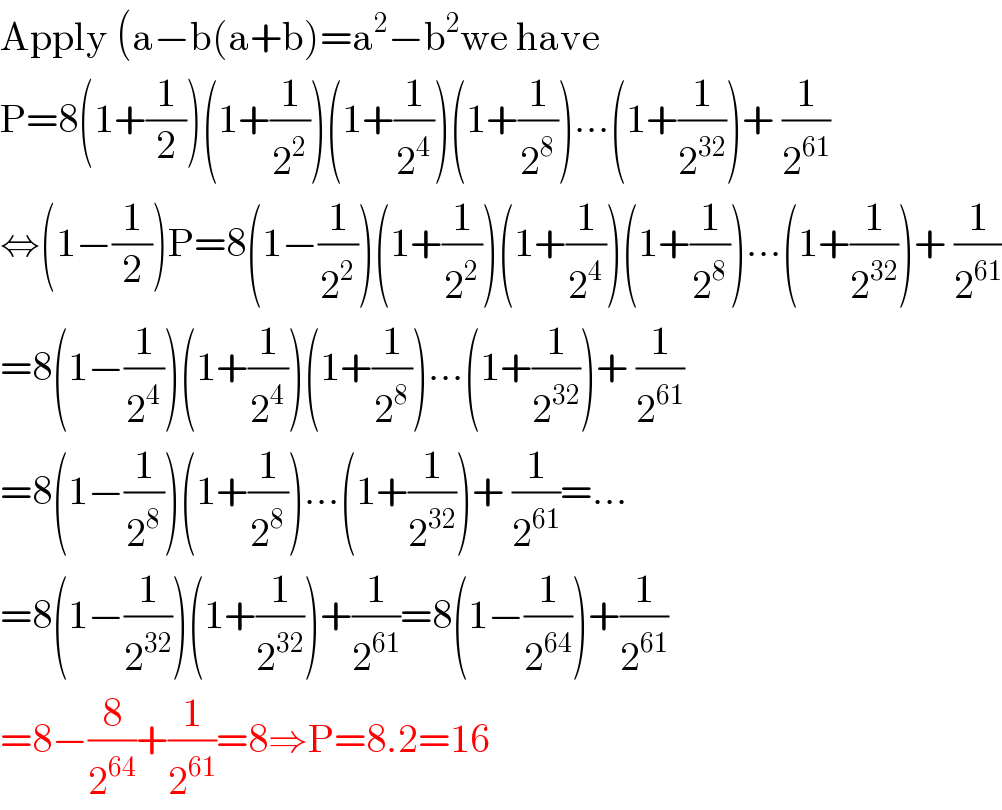
Apply (a−b(a+b)=a^2 −b^2 we have P=8(1+(1/2))(1+(1/2^2 ))(1+(1/2^4 ))(1+(1/2^8 ))...(1+(1/2^(32) ))+ (1/2^(61) ) ⇔(1−(1/2))P=8(1−(1/2^2 ))(1+(1/2^2 ))(1+(1/2^4 ))(1+(1/2^8 ))...(1+(1/2^(32) ))+ (1/2^(61) ) =8(1−(1/2^4 ))(1+(1/2^4 ))(1+(1/2^8 ))...(1+(1/2^(32) ))+ (1/2^(61) ) =8(1−(1/2^8 ))(1+(1/2^8 ))...(1+(1/2^(32) ))+ (1/2^(61) )=... =8(1−(1/2^(32) ))(1+(1/2^(32) ))+(1/2^(61) )=8(1−(1/2^(64) ))+(1/2^(61) ) =8−(8/2^(64) )+(1/2^(61) )=8⇒P=8.2=16
$$\mathrm{Apply}\:\left(\mathrm{a}−\mathrm{b}\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \mathrm{we}\:\mathrm{have}\right. \\ $$$$\mathrm{P}=\mathrm{8}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{8}} }\right)…\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} } \\ $$$$\Leftrightarrow\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{P}=\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{8}} }\right)…\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} } \\ $$$$=\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{8}} }\right)…\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} } \\ $$$$=\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{8}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{8}} }\right)…\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }=… \\ $$$$=\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{32}} }\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }=\mathrm{8}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{64}} }\right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} } \\ $$$$=\mathrm{8}−\frac{\mathrm{8}}{\mathrm{2}^{\mathrm{64}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{61}} }=\mathrm{8}\Rightarrow\mathrm{P}=\mathrm{8}.\mathrm{2}=\mathrm{16} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *