Question Number 96505 by bemath last updated on 02/Jun/20
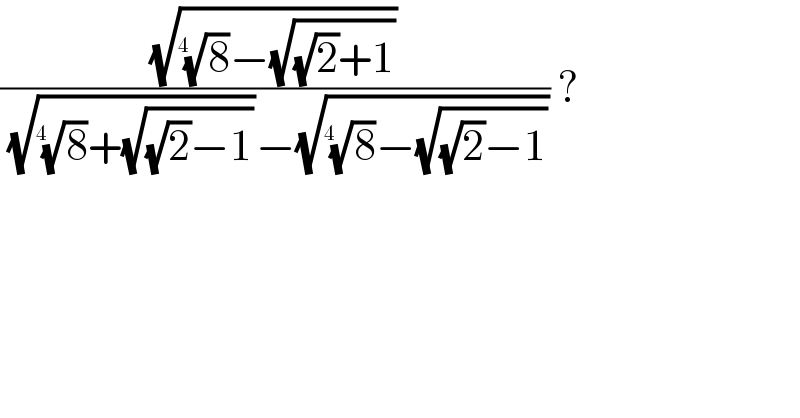
$$\frac{\sqrt{\sqrt[{\mathrm{4}\:\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}}}{\:\sqrt{\sqrt[{\mathrm{4}\:\:}]{\mathrm{8}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}−\sqrt{\sqrt[{\mathrm{4}\:\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}}\:? \\ $$
Commented by bemath last updated on 02/Jun/20

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{you}\:\mathrm{are}\:\mathrm{right} \\ $$
Commented by bobhans last updated on 02/Jun/20
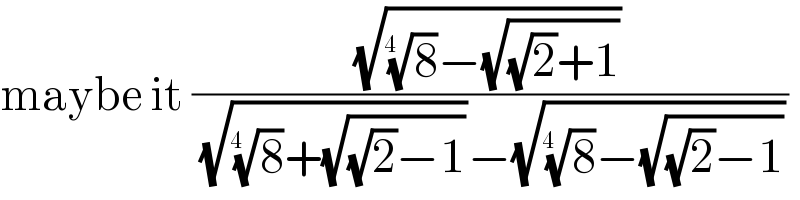
$$\mathrm{maybe}\:\mathrm{it}\:\frac{\sqrt{\sqrt[{\mathrm{4}\:\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}}}{\:\sqrt{\sqrt[{\mathrm{4}\:\:}]{\mathrm{8}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}−\sqrt{\sqrt[{\mathrm{4}\:\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}} \\ $$
Answered by bobhans last updated on 02/Jun/20
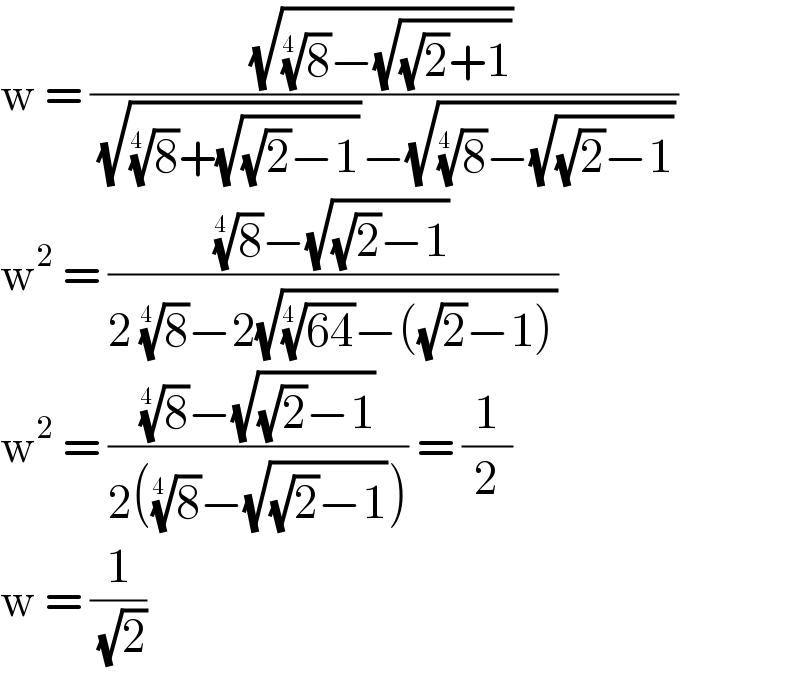
$$\mathrm{w}\:=\:\frac{\sqrt{\sqrt[{\mathrm{4}\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}}}{\:\sqrt{\sqrt[{\mathrm{4}\:}]{\mathrm{8}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}−\sqrt{\sqrt[{\mathrm{4}\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}} \\ $$$$\mathrm{w}^{\mathrm{2}} \:=\:\frac{\sqrt[{\mathrm{4}\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\mathrm{2}\:\sqrt[{\mathrm{4}\:}]{\mathrm{8}}−\mathrm{2}\sqrt{\sqrt[{\mathrm{4}\:}]{\mathrm{64}}−\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}} \\ $$$$\mathrm{w}^{\mathrm{2}} \:=\:\frac{\sqrt[{\mathrm{4}\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\mathrm{2}\left(\sqrt[{\mathrm{4}\:}]{\mathrm{8}}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{w}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\: \\ $$
Answered by 1549442205 last updated on 02/Jun/20
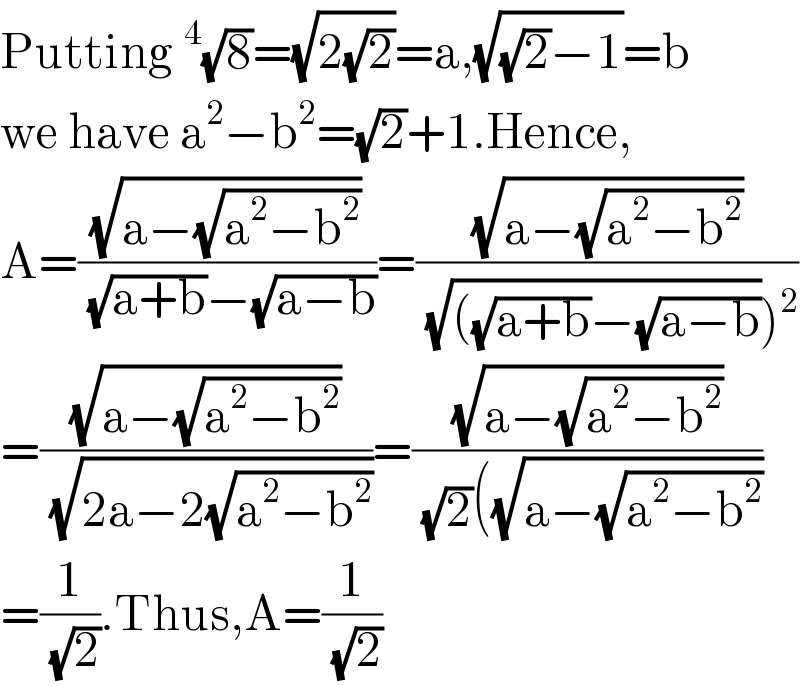
$$\mathrm{Putting}\:^{\mathrm{4}} \sqrt{\mathrm{8}}=\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}=\mathrm{a},\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}=\mathrm{b} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} =\sqrt{\mathrm{2}}+\mathrm{1}.\mathrm{Hence}, \\ $$$$\mathrm{A}=\frac{\sqrt{\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{a}+\mathrm{b}}−\sqrt{\mathrm{a}−\mathrm{b}}}=\frac{\sqrt{\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }}}{\left.\:\sqrt{\left(\sqrt{\mathrm{a}+\mathrm{b}}−\sqrt{\mathrm{a}−\mathrm{b}}\right.}\right)^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{2a}−\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }}}=\frac{\sqrt{\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }}\right.} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}.\mathrm{Thus},\mathrm{A}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$
