Menu Close

8-1-5-9-8-5-9-13-8-9-13-17-1-41-45-49-by-M-A-

Tinku Tara 0 Comments
Pin




Question Number 166707 by amin96 last updated on 25/Feb/22
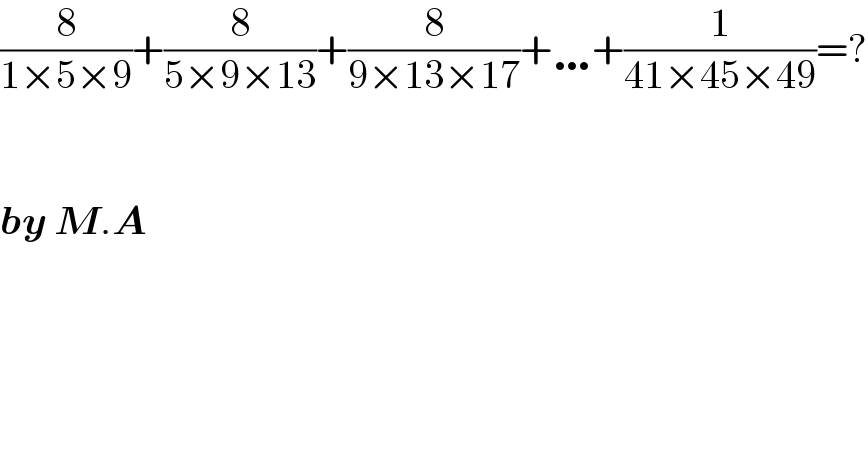
(8/(1×5×9))+(8/(5×9×13))+(8/(9×13×17))+…+(1/(41×45×49))=? by M.A
$$\frac{\mathrm{8}}{\mathrm{1}×\mathrm{5}×\mathrm{9}}+\frac{\mathrm{8}}{\mathrm{5}×\mathrm{9}×\mathrm{13}}+\frac{\mathrm{8}}{\mathrm{9}×\mathrm{13}×\mathrm{17}}+\ldots+\frac{\mathrm{1}}{\mathrm{41}×\mathrm{45}×\mathrm{49}}=? \\ $$$$ \\ $$$$ \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{M}}.\boldsymbol{{A}} \\ $$
Answered by mahdipoor last updated on 25/Feb/22
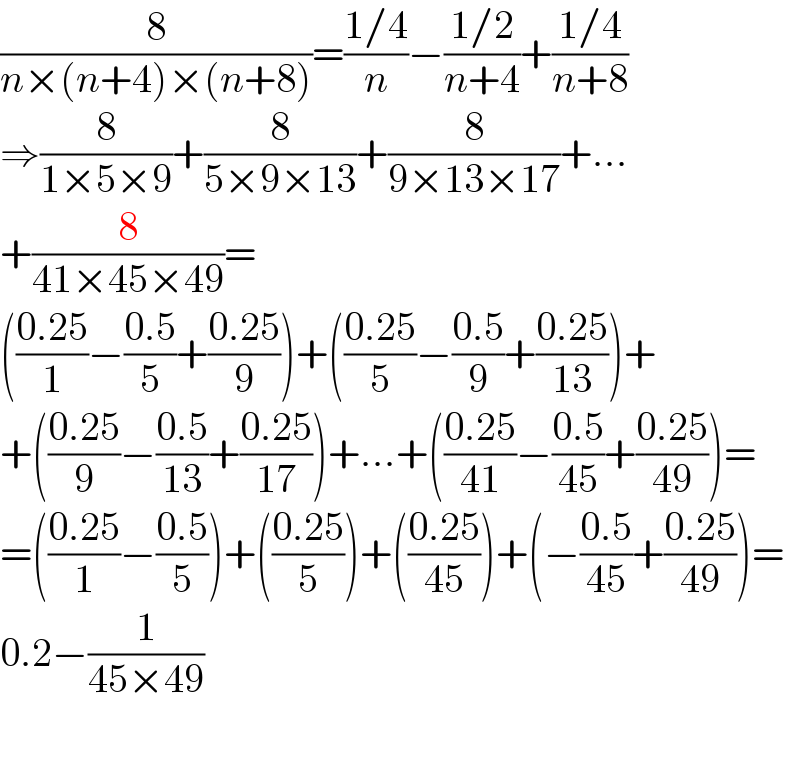
(8/(n×(n+4)×(n+8)))=((1/4)/n)−((1/2)/(n+4))+((1/4)/(n+8)) ⇒(8/(1×5×9))+(8/(5×9×13))+(8/(9×13×17))+... +(8/(41×45×49))= (((0.25)/1)−((0.5)/5)+((0.25)/9))+(((0.25)/5)−((0.5)/9)+((0.25)/(13)))+ +(((0.25)/9)−((0.5)/(13))+((0.25)/(17)))+...+(((0.25)/(41))−((0.5)/(45))+((0.25)/(49)))= =(((0.25)/1)−((0.5)/5))+(((0.25)/5))+(((0.25)/(45)))+(−((0.5)/(45))+((0.25)/(49)))= 0.2−(1/(45×49))
$$\frac{\mathrm{8}}{{n}×\left({n}+\mathrm{4}\right)×\left({n}+\mathrm{8}\right)}=\frac{\mathrm{1}/\mathrm{4}}{{n}}−\frac{\mathrm{1}/\mathrm{2}}{{n}+\mathrm{4}}+\frac{\mathrm{1}/\mathrm{4}}{{n}+\mathrm{8}} \\ $$$$\Rightarrow\frac{\mathrm{8}}{\mathrm{1}×\mathrm{5}×\mathrm{9}}+\frac{\mathrm{8}}{\mathrm{5}×\mathrm{9}×\mathrm{13}}+\frac{\mathrm{8}}{\mathrm{9}×\mathrm{13}×\mathrm{17}}+… \\ $$$$+\frac{\mathrm{8}}{\mathrm{41}×\mathrm{45}×\mathrm{49}}= \\ $$$$\left(\frac{\mathrm{0}.\mathrm{25}}{\mathrm{1}}−\frac{\mathrm{0}.\mathrm{5}}{\mathrm{5}}+\frac{\mathrm{0}.\mathrm{25}}{\mathrm{9}}\right)+\left(\frac{\mathrm{0}.\mathrm{25}}{\mathrm{5}}−\frac{\mathrm{0}.\mathrm{5}}{\mathrm{9}}+\frac{\mathrm{0}.\mathrm{25}}{\mathrm{13}}\right)+ \\ $$$$+\left(\frac{\mathrm{0}.\mathrm{25}}{\mathrm{9}}−\frac{\mathrm{0}.\mathrm{5}}{\mathrm{13}}+\frac{\mathrm{0}.\mathrm{25}}{\mathrm{17}}\right)+…+\left(\frac{\mathrm{0}.\mathrm{25}}{\mathrm{41}}−\frac{\mathrm{0}.\mathrm{5}}{\mathrm{45}}+\frac{\mathrm{0}.\mathrm{25}}{\mathrm{49}}\right)= \\ $$$$=\left(\frac{\mathrm{0}.\mathrm{25}}{\mathrm{1}}−\frac{\mathrm{0}.\mathrm{5}}{\mathrm{5}}\right)+\left(\frac{\mathrm{0}.\mathrm{25}}{\mathrm{5}}\right)+\left(\frac{\mathrm{0}.\mathrm{25}}{\mathrm{45}}\right)+\left(−\frac{\mathrm{0}.\mathrm{5}}{\mathrm{45}}+\frac{\mathrm{0}.\mathrm{25}}{\mathrm{49}}\right)= \\ $$$$\mathrm{0}.\mathrm{2}−\frac{\mathrm{1}}{\mathrm{45}×\mathrm{49}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *