8-x-1-3-x-2-

Question Number 95159 by i jagooll last updated on 23/May/20

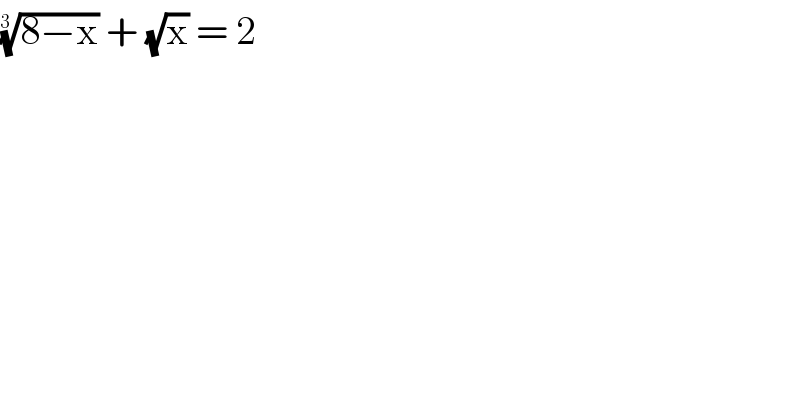
$$\sqrt[{\mathrm{3}\:\:}]{\mathrm{8}−\mathrm{x}}\:+\:\sqrt{\mathrm{x}}\:=\:\mathrm{2}\: \\ $$

Commented by hknkrc46 last updated on 23/May/20

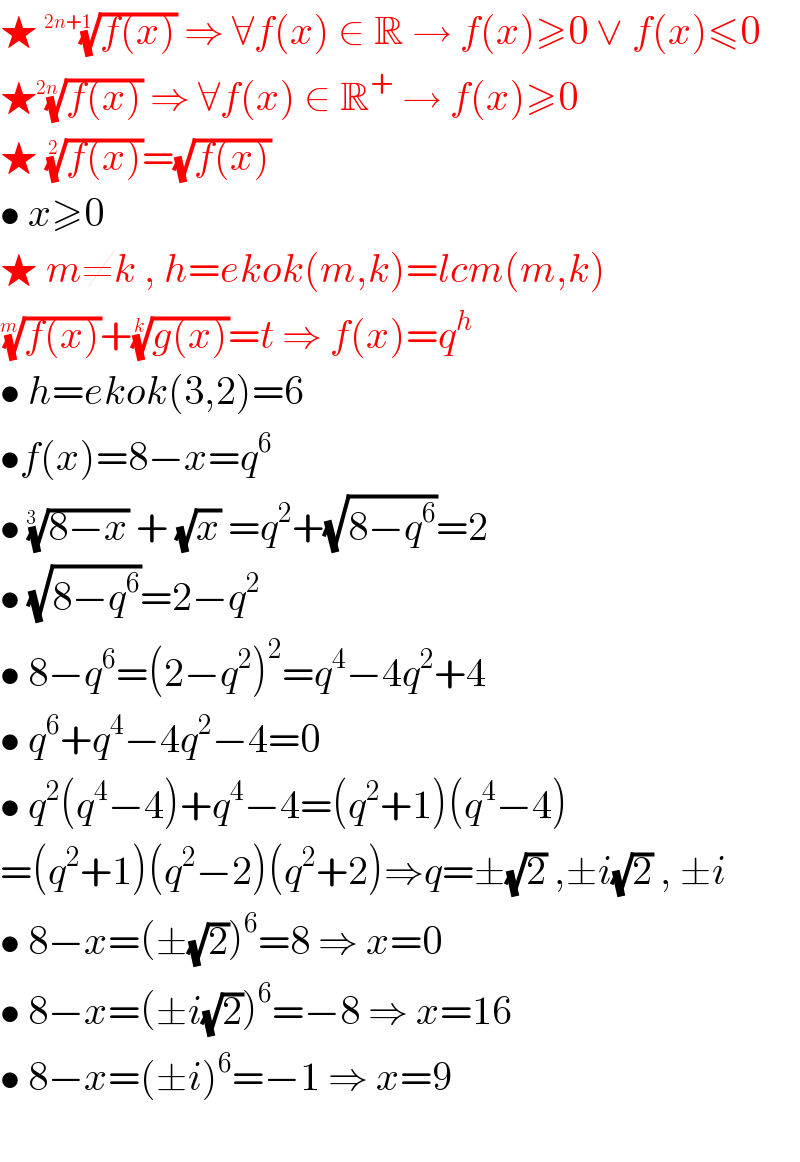
★ ((f(x)))^(1/(2n+1)) ⇒ ∀f(x) ∈ R → f(x)≥0 ∨ f(x)≤0 ★((f(x)))^(1/(2n)) ⇒ ∀f(x) ∈ R^+ → f(x)≥0 ★ ((f(x)))^(1/2) =(√(f(x))) • x≥0 ★ m≠k , h=ekok(m,k)=lcm(m,k) ((f(x)))^(1/m) +((g(x)))^(1/k) =t ⇒ f(x)=q^h • h=ekok(3,2)=6 •f(x)=8−x=q^6 • ((8−x))^(1/(3 )) + (√x) =q^2 +(√(8−q^6 ))=2 • (√(8−q^6 ))=2−q^2 • 8−q^6 =(2−q^2 )^2 =q^4 −4q^2 +4 • q^6 +q^4 −4q^2 −4=0 • q^2 (q^4 −4)+q^4 −4=(q^2 +1)(q^4 −4) =(q^2 +1)(q^2 −2)(q^2 +2)⇒q=±(√2) ,±i(√2) , ±i • 8−x=(±(√2))^6 =8 ⇒ x=0 • 8−x=(±i(√2))^6 =−8 ⇒ x=16 • 8−x=(±i)^6 =−1 ⇒ x=9

$$\bigstar\:\sqrt[{\mathrm{2}{n}+\mathrm{1}}]{{f}\left({x}\right)}\:\Rightarrow\:\forall{f}\left({x}\right)\:\in\:\mathbb{R}\:\rightarrow\:{f}\left({x}\right)\geqslant\mathrm{0}\:\vee\:{f}\left({x}\right)\leqslant\mathrm{0} \\ $$$$\bigstar\sqrt[{\mathrm{2}{n}}]{{f}\left({x}\right)}\:\Rightarrow\:\forall{f}\left({x}\right)\:\in\:\mathbb{R}^{+} \:\rightarrow\:{f}\left({x}\right)\geqslant\mathrm{0} \\ $$$$\bigstar\:\sqrt[{\mathrm{2}}]{{f}\left({x}\right)}=\sqrt{{f}\left({x}\right)} \\ $$$$\bullet\:{x}\geqslant\mathrm{0} \\ $$$$\bigstar\:{m}\neq{k}\:,\:{h}={ekok}\left({m},{k}\right)={lcm}\left({m},{k}\right) \\ $$$$\sqrt[{{m}}]{{f}\left({x}\right)}+\sqrt[{{k}}]{{g}\left({x}\right)}={t}\:\Rightarrow\:{f}\left({x}\right)={q}^{{h}} \: \\ $$$$\bullet\:{h}={ekok}\left(\mathrm{3},\mathrm{2}\right)=\mathrm{6} \\ $$$$\bullet{f}\left({x}\right)=\mathrm{8}−{x}={q}^{\mathrm{6}} \\ $$$$\bullet\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{8}−{x}}\:+\:\sqrt{{x}}\:={q}^{\mathrm{2}} +\sqrt{\mathrm{8}−{q}^{\mathrm{6}} }=\mathrm{2} \\ $$$$\bullet\:\sqrt{\mathrm{8}−{q}^{\mathrm{6}} }=\mathrm{2}−{q}^{\mathrm{2}} \\ $$$$\bullet\:\mathrm{8}−{q}^{\mathrm{6}} =\left(\mathrm{2}−{q}^{\mathrm{2}} \right)^{\mathrm{2}} ={q}^{\mathrm{4}} −\mathrm{4}{q}^{\mathrm{2}} +\mathrm{4} \\ $$$$\bullet\:{q}^{\mathrm{6}} +{q}^{\mathrm{4}} −\mathrm{4}{q}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$$\bullet\:{q}^{\mathrm{2}} \left({q}^{\mathrm{4}} −\mathrm{4}\right)+{q}^{\mathrm{4}} −\mathrm{4}=\left({q}^{\mathrm{2}} +\mathrm{1}\right)\left({q}^{\mathrm{4}} −\mathrm{4}\right) \\ $$$$=\left({q}^{\mathrm{2}} +\mathrm{1}\right)\left({q}^{\mathrm{2}} −\mathrm{2}\right)\left({q}^{\mathrm{2}} +\mathrm{2}\right)\Rightarrow{q}=\pm\sqrt{\mathrm{2}}\:,\pm{i}\sqrt{\mathrm{2}}\:,\:\pm{i} \\ $$$$\bullet\:\mathrm{8}−{x}=\left(\pm\sqrt{\mathrm{2}}\right)^{\mathrm{6}} =\mathrm{8}\:\Rightarrow\:{x}=\mathrm{0} \\ $$$$\bullet\:\mathrm{8}−{x}=\left(\pm{i}\sqrt{\mathrm{2}}\right)^{\mathrm{6}} =−\mathrm{8}\:\Rightarrow\:{x}=\mathrm{16} \\ $$$$\bullet\:\mathrm{8}−{x}=\left(\pm{i}\right)^{\mathrm{6}} =−\mathrm{1}\:\Rightarrow\:{x}=\mathrm{9} \\ $$$$ \\ $$

Answered by bobhans last updated on 23/May/20

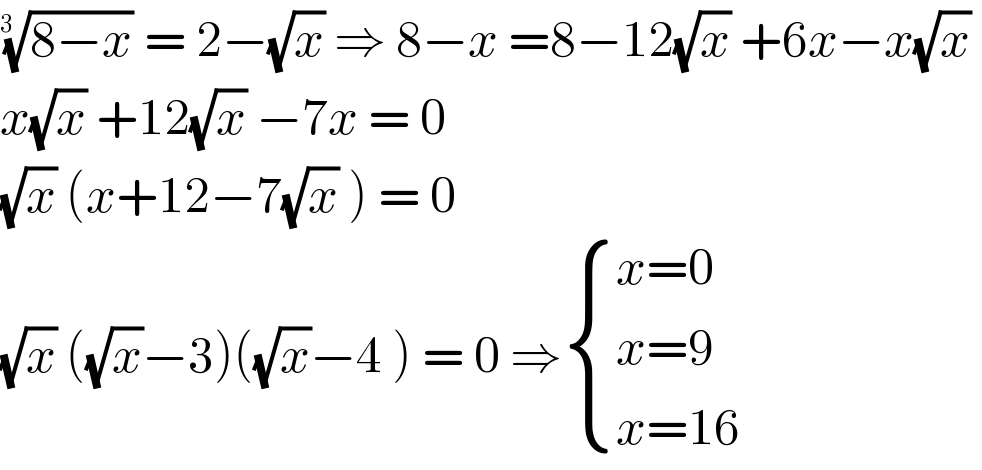
((8−x))^(1/(3 )) = 2−(√x) ⇒ 8−x =8−12(√x) +6x−x(√x) x(√x) +12(√x) −7x = 0 (√x) (x+12−7(√x) ) = 0 (√x) ((√x)−3)((√x)−4 ) = 0 ⇒ { ((x=0)),((x=9)),((x=16)) :}

$$\sqrt[{\mathrm{3}\:\:}]{\mathrm{8}−{x}}\:=\:\mathrm{2}−\sqrt{{x}}\:\Rightarrow\:\mathrm{8}−{x}\:=\mathrm{8}−\mathrm{12}\sqrt{{x}}\:+\mathrm{6}{x}−{x}\sqrt{{x}}\: \\ $$$${x}\sqrt{{x}}\:+\mathrm{12}\sqrt{{x}}\:−\mathrm{7}{x}\:=\:\mathrm{0} \\ $$$$\sqrt{{x}}\:\left({x}+\mathrm{12}−\mathrm{7}\sqrt{{x}}\:\right)\:=\:\mathrm{0} \\ $$$$\sqrt{{x}}\:\left(\sqrt{{x}}−\mathrm{3}\right)\left(\sqrt{{x}}−\mathrm{4}\:\right)\:=\:\mathrm{0}\:\Rightarrow\begin{cases}{{x}=\mathrm{0}}\\{{x}=\mathrm{9}}\\{{x}=\mathrm{16}}\end{cases} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply