Question Number 92242 by john santu last updated on 05/May/20

$$\frac{\mathrm{8}^{{x}} +\mathrm{27}^{{x}} }{\mathrm{12}^{{x}} +\mathrm{18}^{{x}} }\:=\:\frac{\mathrm{7}}{\mathrm{6}}\: \\ $$$${x}\:=\:? \\ $$
Commented by john santu last updated on 05/May/20
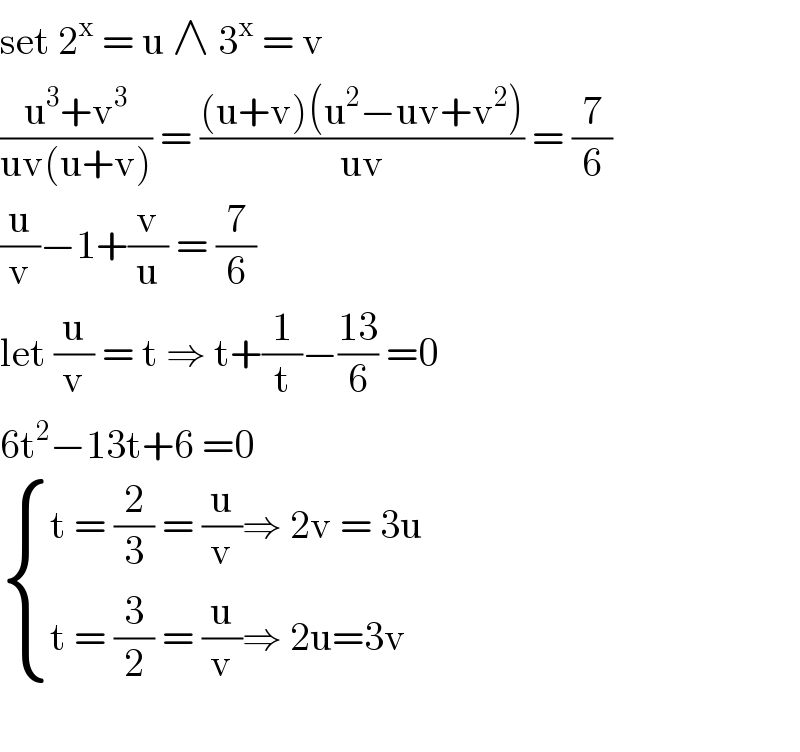
$$\mathrm{set}\:\mathrm{2}^{\mathrm{x}} \:=\:\mathrm{u}\:\wedge\:\mathrm{3}^{\mathrm{x}} \:=\:\mathrm{v}\: \\ $$$$\frac{\mathrm{u}^{\mathrm{3}} +\mathrm{v}^{\mathrm{3}} }{\mathrm{uv}\left(\mathrm{u}+\mathrm{v}\right)}\:=\:\frac{\left(\mathrm{u}+\mathrm{v}\right)\left(\mathrm{u}^{\mathrm{2}} −\mathrm{uv}+\mathrm{v}^{\mathrm{2}} \right)}{\mathrm{uv}}\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\frac{\mathrm{u}}{\mathrm{v}}−\mathrm{1}+\frac{\mathrm{v}}{\mathrm{u}}\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\mathrm{let}\:\frac{\mathrm{u}}{\mathrm{v}}\:=\:\mathrm{t}\:\Rightarrow\:\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{13}}{\mathrm{6}}\:=\mathrm{0} \\ $$$$\mathrm{6t}^{\mathrm{2}} −\mathrm{13t}+\mathrm{6}\:=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{t}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:=\:\frac{\mathrm{u}}{\mathrm{v}}\Rightarrow\:\mathrm{2v}\:=\:\mathrm{3u}}\\{\mathrm{t}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\:=\:\frac{\mathrm{u}}{\mathrm{v}}\Rightarrow\:\mathrm{2u}=\mathrm{3v}}\end{cases} \\ $$$$ \\ $$
Commented by john santu last updated on 05/May/20
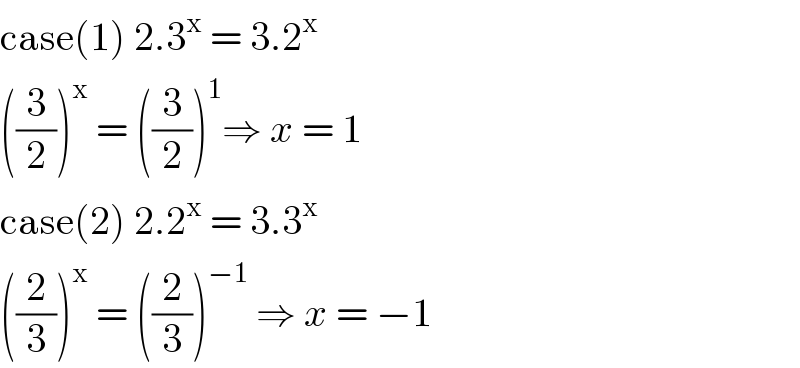
$$\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{2}.\mathrm{3}^{\mathrm{x}} \:=\:\mathrm{3}.\mathrm{2}^{\mathrm{x}} \: \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{x}} \:=\:\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{1}} \Rightarrow\:{x}\:=\:\mathrm{1} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{2}.\mathrm{2}^{\mathrm{x}} \:=\:\mathrm{3}.\mathrm{3}^{\mathrm{x}} \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \:=\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{−\mathrm{1}} \:\Rightarrow\:{x}\:=\:−\mathrm{1}\: \\ $$
