Question Number 178113 by Acem last updated on 12/Oct/22

$$\:\mathrm{8}\:{yellow},\:\mathrm{8}\:{red},\:\mathrm{8}\:{green}\:{and}\:\mathrm{8}\:{blue}\:{cards},\: \\ $$$${each}\:{grouo}\:{is}\:{numbered}\:{from}\:\mathrm{1}\:{to}\:\mathrm{8}\:. \\ $$$$\:{We}\:{want}\:{to}\:{know}\:{how}\:{many}\:{pulls}\:{contain} \\ $$$$\:{at}\:{least}\:{one}\:{card}\:{with}\:{number}\:\mathrm{1}\:{through} \\ $$$$\:{pull}\:{processes}\:\mathrm{5}\:{cards}\:{each}\:{time} \\ $$$$ \\ $$$$ \\ $$
Answered by mr W last updated on 13/Oct/22
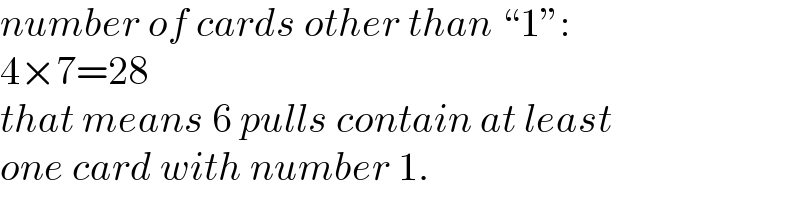
$${number}\:{of}\:{cards}\:{other}\:{than}\:“\mathrm{1}'': \\ $$$$\mathrm{4}×\mathrm{7}=\mathrm{28} \\ $$$${that}\:{means}\:\mathrm{6}\:{pulls}\:{contain}\:{at}\:{least} \\ $$$${one}\:{card}\:{with}\:{number}\:\mathrm{1}. \\ $$
Commented by Acem last updated on 13/Oct/22

$$ \\ $$$${To}\:{get}\:{at}\:{least}\:{one}\:{card}\:{with}\:{num}.\:\mathrm{1}\:{means} \\ $$$$\:{we}\:{may}\:{have}\:{one}\:{card}\:{or}\:{two}…\:{or}\:{four}_{{num}.\:\mathrm{1}} \\ $$$$\:{Yes}\:{we}\:{have}\:\mathrm{28}\:{cards}\:{other}\:{than}\:\mathrm{1},\:{so}\:{we} \\ $$$$\:{can}\:{subtract}\:{the}\:{C}_{\mathrm{5}} ^{\:\mathrm{28}} \:_{{other}\:{than}\:\mathrm{1}} \:{from}\:{the}\:{total} \\ $$$$\:{ways}\:{of}\:{pull}\:{any}\:{five}\:{of}\:\mathrm{32}\:{cards}\:{i}.{e}. \\ $$$$ \\ $$$${NumPulls}_{{num}.\:\mathrm{1}\:{at}\:{least}} \:=\:{C}_{\mathrm{5}} ^{\:\mathrm{32}} \:−\:{C}_{\mathrm{5}} ^{\:\mathrm{28}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{103}\:\mathrm{096}\:{pulls} \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 13/Oct/22
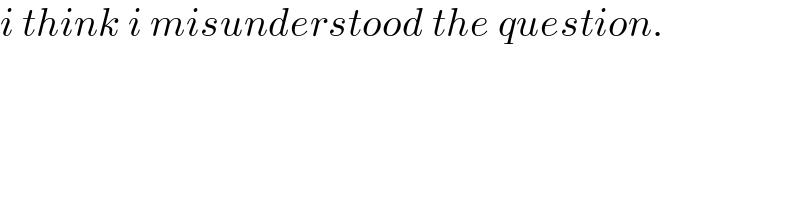
$${i}\:{think}\:{i}\:{misunderstood}\:{the}\:{question}. \\ $$
Commented by Tawa11 last updated on 13/Oct/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by Acem last updated on 13/Oct/22
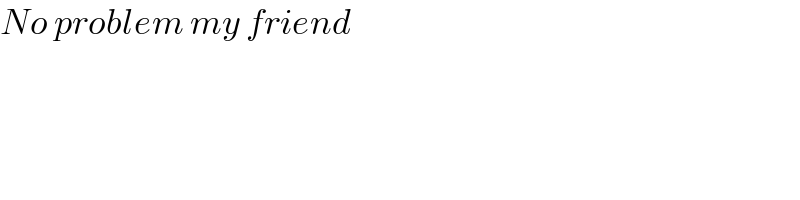
$${No}\:{problem}\:{my}\:{friend} \\ $$
Commented by Acem last updated on 13/Oct/22

$${You}'{re}\:{very}\:{much}\:{welcome} \\ $$
