Question Number 58776 by George Mark Samuel last updated on 29/Apr/19
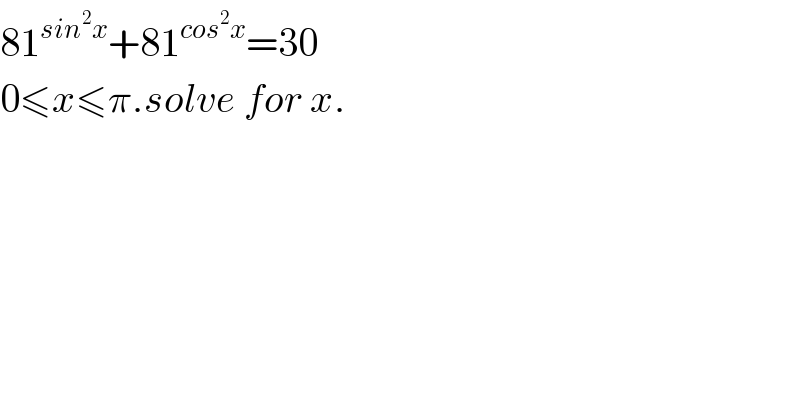
$$\mathrm{81}^{{sin}^{\mathrm{2}} {x}} +\mathrm{81}^{{cos}^{\mathrm{2}} {x}} =\mathrm{30} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\pi.{solve}\:{for}\:{x}. \\ $$
Answered by behi83417@gmail.com last updated on 29/Apr/19
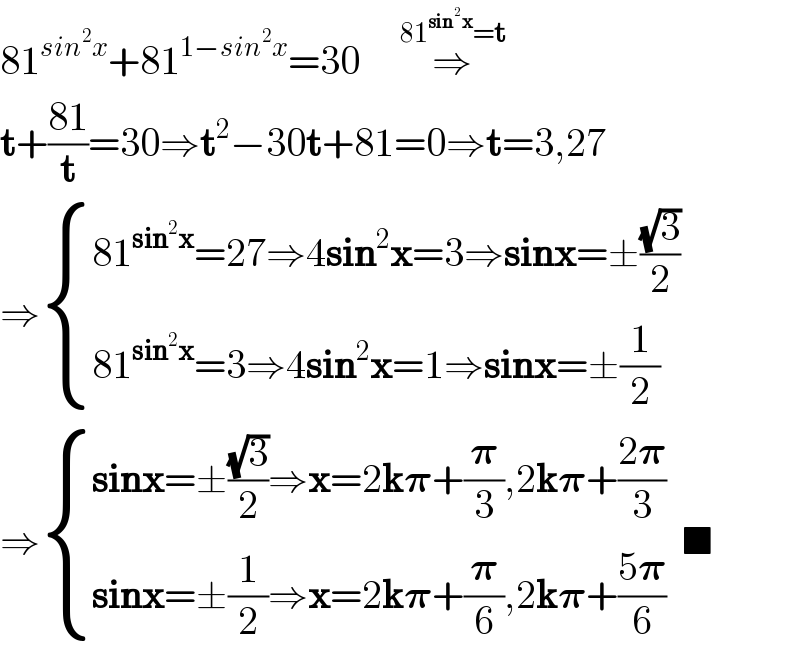
$$\mathrm{81}^{{sin}^{\mathrm{2}} {x}} +\mathrm{81}^{\mathrm{1}−{sin}^{\mathrm{2}} {x}} =\mathrm{30}\:\:\:\:\:\overset{\mathrm{81}^{\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} =\boldsymbol{\mathrm{t}}} {\Rightarrow} \\ $$$$\boldsymbol{\mathrm{t}}+\frac{\mathrm{81}}{\boldsymbol{\mathrm{t}}}=\mathrm{30}\Rightarrow\boldsymbol{\mathrm{t}}^{\mathrm{2}} −\mathrm{30}\boldsymbol{\mathrm{t}}+\mathrm{81}=\mathrm{0}\Rightarrow\boldsymbol{\mathrm{t}}=\mathrm{3},\mathrm{27} \\ $$$$\Rightarrow\begin{cases}{\mathrm{81}^{\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} =\mathrm{27}\Rightarrow\mathrm{4}\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}=\mathrm{3}\Rightarrow\boldsymbol{\mathrm{sinx}}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{\mathrm{81}^{\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} =\mathrm{3}\Rightarrow\mathrm{4}\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}=\mathrm{1}\Rightarrow\boldsymbol{\mathrm{sinx}}=\pm\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\boldsymbol{\mathrm{sinx}}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\Rightarrow\boldsymbol{\mathrm{x}}=\mathrm{2}\boldsymbol{\mathrm{k}\pi}+\frac{\boldsymbol{\pi}}{\mathrm{3}},\mathrm{2}\boldsymbol{\mathrm{k}\pi}+\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{3}}}\\{\boldsymbol{\mathrm{sinx}}=\pm\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\boldsymbol{\mathrm{x}}=\mathrm{2}\boldsymbol{\mathrm{k}\pi}+\frac{\boldsymbol{\pi}}{\mathrm{6}},\mathrm{2}\boldsymbol{\mathrm{k}\pi}+\frac{\mathrm{5}\boldsymbol{\pi}}{\mathrm{6}}}\end{cases}\:\:\blacksquare \\ $$
