Question Number 168664 by cortano1 last updated on 15/Apr/22
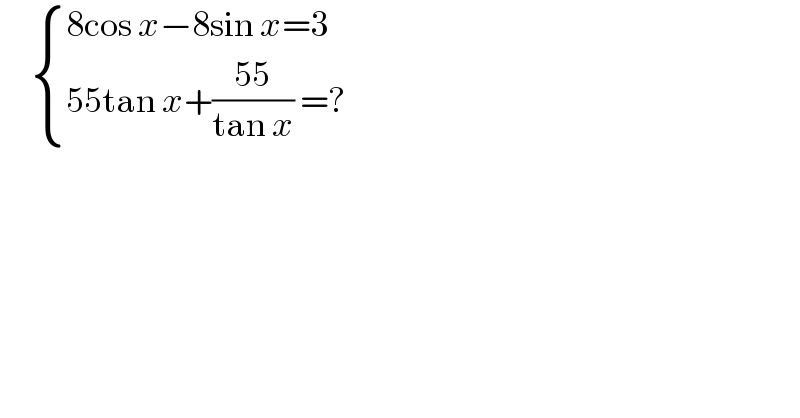
$$\:\:\:\:\:\begin{cases}{\mathrm{8cos}\:{x}−\mathrm{8sin}\:{x}=\mathrm{3}}\\{\mathrm{55tan}\:{x}+\frac{\mathrm{55}}{\mathrm{tan}\:{x}}\:=?}\end{cases} \\ $$
Answered by greogoury55 last updated on 15/Apr/22
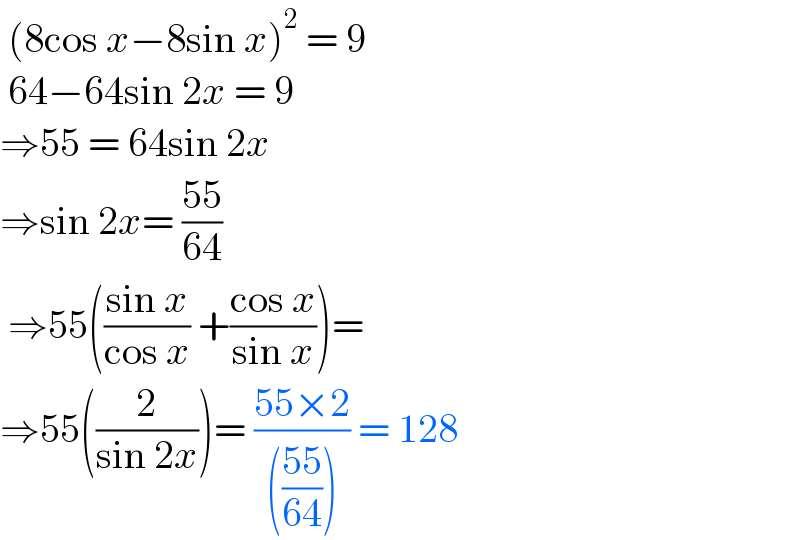
$$\:\left(\mathrm{8cos}\:{x}−\mathrm{8sin}\:{x}\right)^{\mathrm{2}} \:=\:\mathrm{9} \\ $$$$\:\mathrm{64}−\mathrm{64sin}\:\mathrm{2}{x}\:=\:\mathrm{9} \\ $$$$\Rightarrow\mathrm{55}\:=\:\mathrm{64sin}\:\mathrm{2}{x} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}{x}=\:\frac{\mathrm{55}}{\mathrm{64}} \\ $$$$\:\Rightarrow\mathrm{55}\left(\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\:+\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}\right)= \\ $$$$\Rightarrow\mathrm{55}\left(\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{2}{x}}\right)=\:\frac{\mathrm{55}×\mathrm{2}}{\left(\frac{\mathrm{55}}{\mathrm{64}}\right)}\:=\:\mathrm{128}\: \\ $$
