Question Number 147640 by mathdanisur last updated on 22/Jul/21
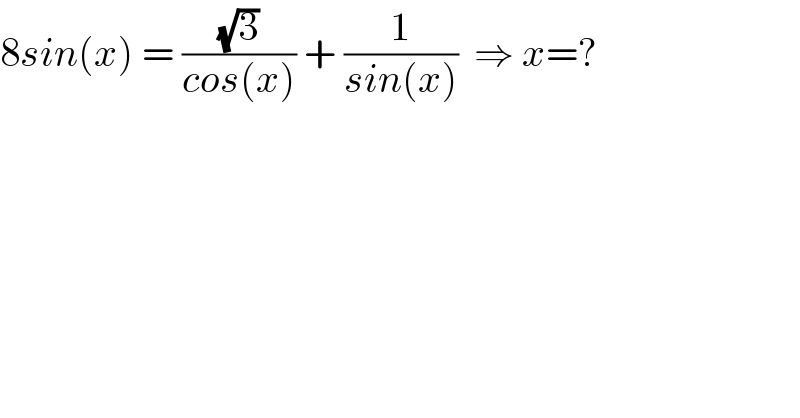
$$\mathrm{8}{sin}\left({x}\right)\:=\:\frac{\sqrt{\mathrm{3}}}{{cos}\left({x}\right)}\:+\:\frac{\mathrm{1}}{{sin}\left({x}\right)}\:\:\Rightarrow\:{x}=? \\ $$
Answered by gsk2684 last updated on 25/Jul/21
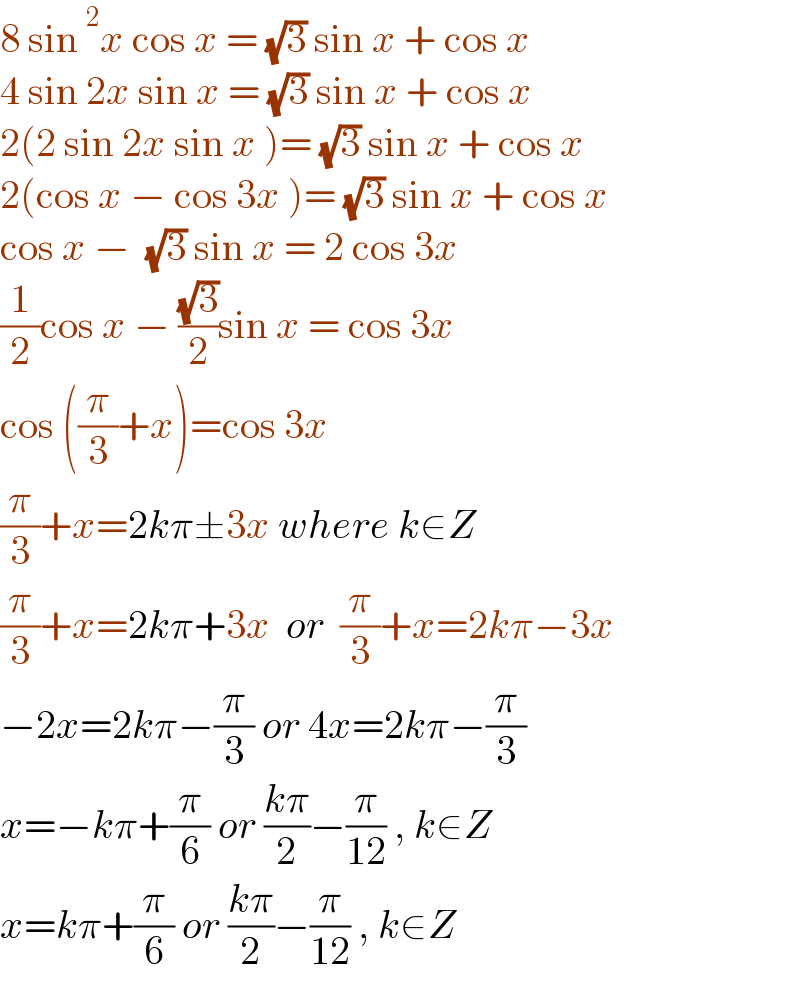
$$\mathrm{8}\:\mathrm{sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:{x}\:=\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x} \\ $$$$\mathrm{4}\:\mathrm{sin}\:\mathrm{2}{x}\:\mathrm{sin}\:{x}\:=\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x} \\ $$$$\mathrm{2}\left(\mathrm{2}\:\mathrm{sin}\:\mathrm{2}{x}\:\mathrm{sin}\:{x}\:\right)=\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x} \\ $$$$\mathrm{2}\left(\mathrm{cos}\:{x}\:−\:\mathrm{cos}\:\mathrm{3}{x}\:\right)=\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x} \\ $$$$\mathrm{cos}\:{x}\:−\:\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:{x}\:=\:\mathrm{2}\:\mathrm{cos}\:\mathrm{3}{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{x}\:−\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:{x}\:=\:\mathrm{cos}\:\mathrm{3}{x} \\ $$$$\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}+{x}\right)=\mathrm{cos}\:\mathrm{3}{x} \\ $$$$\frac{\pi}{\mathrm{3}}+{x}=\mathrm{2}{k}\pi\pm\mathrm{3}{x}\:{where}\:{k}\in{Z} \\ $$$$\frac{\pi}{\mathrm{3}}+{x}=\mathrm{2}{k}\pi+\mathrm{3}{x}\:\:{or}\:\:\frac{\pi}{\mathrm{3}}+{x}=\mathrm{2}{k}\pi−\mathrm{3}{x}\: \\ $$$$−\mathrm{2}{x}=\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{3}}\:{or}\:\mathrm{4}{x}=\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{3}} \\ $$$${x}=−{k}\pi+\frac{\pi}{\mathrm{6}}\:{or}\:\frac{{k}\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{12}}\:,\:{k}\in{Z} \\ $$$${x}={k}\pi+\frac{\pi}{\mathrm{6}}\:{or}\:\frac{{k}\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{12}}\:,\:{k}\in{Z} \\ $$
Commented by mathdanisur last updated on 22/Jul/21

$${Thank}\:{you}\:{Sir} \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${thankyou}\:{Sir} \\ $$
Commented by mathdanisur last updated on 23/Jul/21

$${answer}\:\frac{\pi}{\mathrm{6}}\:+\:\pi{k} \\ $$
Commented by gsk2684 last updated on 25/Jul/21
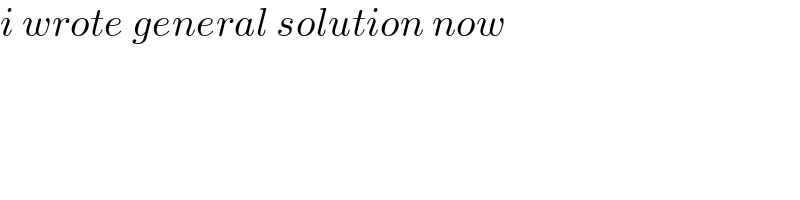
$${i}\:{wrote}\:{general}\:{solution}\:{now} \\ $$
