Menu Close

8x-3-2n-8x-3-2n-63-

Tinku Tara 0 Comments
Pin




Question Number 25246 by ibraheem160 last updated on 06/Dec/17
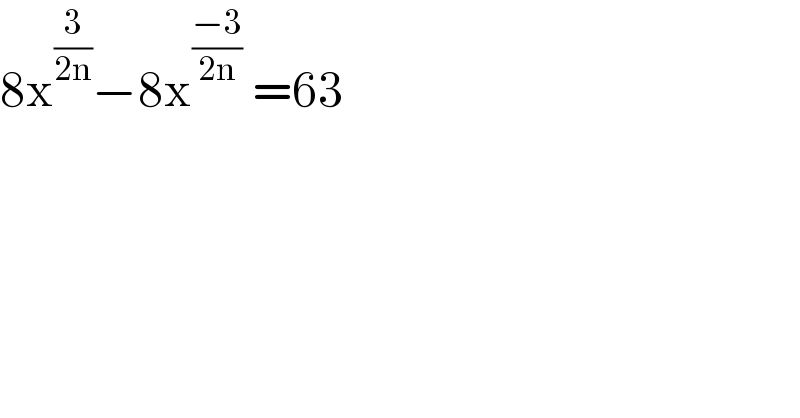
8x^(3/(2n)) −8x^((−3)/(2n)) =63
$$\mathrm{8x}^{\frac{\mathrm{3}}{\mathrm{2n}}} −\mathrm{8x}^{\frac{−\mathrm{3}}{\mathrm{2n}}} \:=\mathrm{63} \\ $$
Answered by Rasheed.Sindhi last updated on 07/Dec/17
8x^(3/(2n)) −8x^((−3)/(2n)) =63 8x^(3/2n) −8((1/x^(3/2n) ))=63 Let x^(3/2n) =y 8y−(8/y)=63 8y^2 −63y−8=0 y=((63±(√(3969+256)))/(16))x y=((63±(√(4225)))/(16)) y=((63±65)/(16))=8,−1/8 x^(3/2n) =8 or x^(3/2n) =−1/8 x=(2^3 )^(2n/3) or x=(2^(−3) )^(2n/3) x=2^(2n) ,2^(−2n) =4^n ,4^(−n)
$$\mathrm{8x}^{\frac{\mathrm{3}}{\mathrm{2n}}} −\mathrm{8x}^{\frac{−\mathrm{3}}{\mathrm{2n}}} \:=\mathrm{63} \\ $$$$\mathrm{8x}^{\mathrm{3}/\mathrm{2n}} −\mathrm{8}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}/\mathrm{2n}} }\right)=\mathrm{63} \\ $$$$\mathrm{Let}\:\mathrm{x}^{\mathrm{3}/\mathrm{2n}} =\mathrm{y} \\ $$$$\mathrm{8y}−\frac{\mathrm{8}}{\mathrm{y}}=\mathrm{63} \\ $$$$\mathrm{8y}^{\mathrm{2}} −\mathrm{63y}−\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{y}=\frac{\mathrm{63}\pm\sqrt{\mathrm{3969}+\mathrm{256}}}{\mathrm{16}}\mathrm{x} \\ $$$$\mathrm{y}=\frac{\mathrm{63}\pm\sqrt{\mathrm{4225}}}{\mathrm{16}} \\ $$$$\mathrm{y}=\frac{\mathrm{63}\pm\mathrm{65}}{\mathrm{16}}=\mathrm{8},−\mathrm{1}/\mathrm{8} \\ $$$$\mathrm{x}^{\mathrm{3}/\mathrm{2n}} =\mathrm{8}\:\:\mathrm{or}\:\:\mathrm{x}^{\mathrm{3}/\mathrm{2n}} =−\mathrm{1}/\mathrm{8} \\ $$$$\mathrm{x}=\left(\mathrm{2}^{\mathrm{3}} \right)^{\mathrm{2n}/\mathrm{3}} \:\:\mathrm{or}\:\:\mathrm{x}=\left(\mathrm{2}^{−\mathrm{3}} \right)^{\mathrm{2n}/\mathrm{3}} \\ $$$$\mathrm{x}=\mathrm{2}^{\mathrm{2n}} ,\mathrm{2}^{−\mathrm{2n}} \\ $$$$\:\:\:=\mathrm{4}^{\mathrm{n}} ,\mathrm{4}^{−\mathrm{n}} \\ $$
Commented by ibraheem160 last updated on 07/Dec/17
how did you inverse the power?
$$\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\:\mathrm{inverse}\:\mathrm{the}\:\mathrm{power}? \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 07/Dec/17
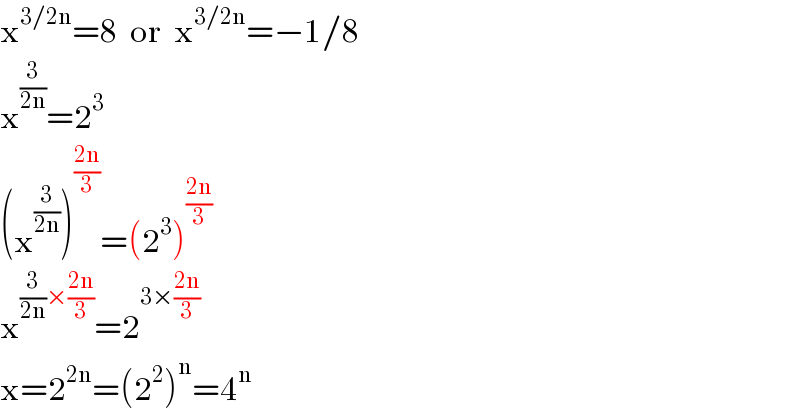
x^(3/2n) =8 or x^(3/2n) =−1/8 x^(3/(2n)) =2^3 (x^(3/(2n)) )^((2n)/3) =(2^3 )^((2n)/3) x^((3/(2n))×((2n)/3)) =2^(3×((2n)/3)) x=2^(2n) =(2^2 )^n =4^n
$$\mathrm{x}^{\mathrm{3}/\mathrm{2n}} =\mathrm{8}\:\:\mathrm{or}\:\:\mathrm{x}^{\mathrm{3}/\mathrm{2n}} =−\mathrm{1}/\mathrm{8} \\ $$$$\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2n}}} =\mathrm{2}^{\mathrm{3}} \\ $$$$\left(\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2n}}} \right)^{\frac{\mathrm{2n}}{\mathrm{3}}} =\left(\mathrm{2}^{\mathrm{3}} \right)^{\frac{\mathrm{2n}}{\mathrm{3}}} \\ $$$$\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2n}}×\frac{\mathrm{2n}}{\mathrm{3}}} =\mathrm{2}^{\mathrm{3}×\frac{\mathrm{2n}}{\mathrm{3}}} \\ $$$$\mathrm{x}=\mathrm{2}^{\mathrm{2n}} =\left(\mathrm{2}^{\mathrm{2}} \right)^{\mathrm{n}} =\mathrm{4}^{\mathrm{n}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *