Question Number 89955 by swizanjere@gmail.com last updated on 20/Apr/20
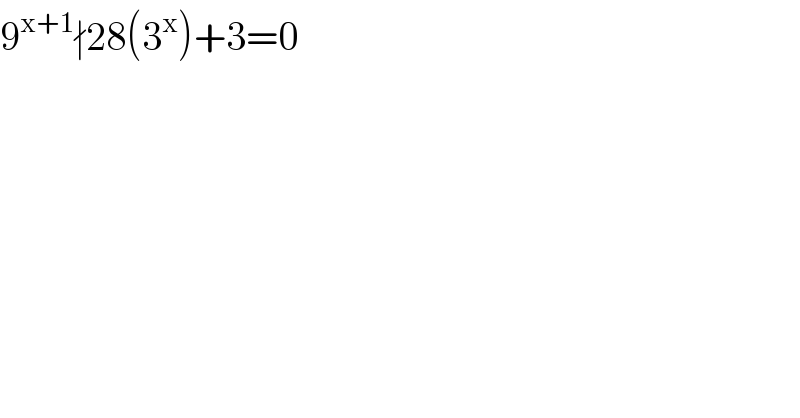
$$\mathrm{9}^{\mathrm{x}+\mathrm{1}} \nmid\mathrm{28}\left(\mathrm{3}^{\mathrm{x}} \right)+\mathrm{3}=\mathrm{0} \\ $$
Commented by jagoll last updated on 20/Apr/20

$$\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{notation} \\ $$$$\nmid\:? \\ $$
Commented by Rio Michael last updated on 20/Apr/20
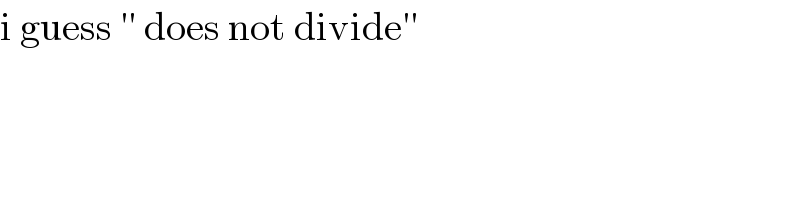
$$\mathrm{i}\:\mathrm{guess}\:''\:\mathrm{does}\:\mathrm{not}\:\mathrm{divide}'' \\ $$
Answered by john santu last updated on 20/Apr/20
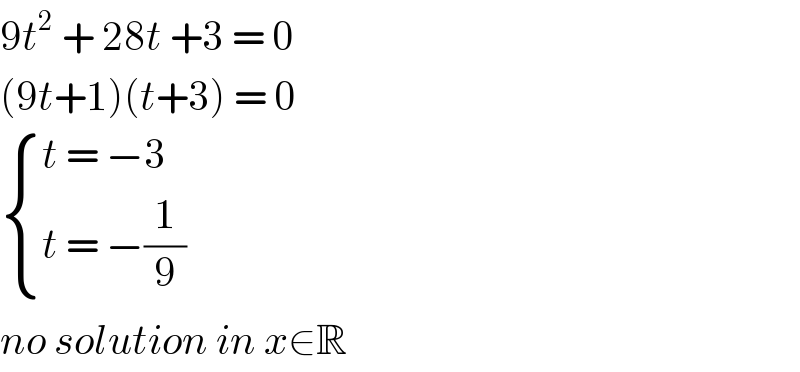
$$\mathrm{9}{t}^{\mathrm{2}} \:+\:\mathrm{28}{t}\:+\mathrm{3}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{9}{t}+\mathrm{1}\right)\left({t}+\mathrm{3}\right)\:=\:\mathrm{0} \\ $$$$\begin{cases}{{t}\:=\:−\mathrm{3}\:}\\{{t}\:=\:−\frac{\mathrm{1}}{\mathrm{9}}\:}\end{cases}\:\: \\ $$$${no}\:{solution}\:{in}\:{x}\in\mathbb{R}\: \\ $$
